集合
映射
函数
极限
无穷小与无穷大
极限的运算法则
极限存在的准则&两个重要的极限
函数的连续性和间断点
闭区间上连续的函数的性质
数列的极限
我们先来认识极限的概念.“极”是“最终的,最高的”,比如极点;“限”是“某一数量或某地”,比如“城区汽车限速60 km/h”,“60 km/h”就是限;一直往前走你会到达学校“南门”,南门就是限.极限就是最终的数量、最终的地点等.无论“最终的数量”还是“最终的地点”,极限都是一个名词, 都是动态地达到的数量或地点,是从远到近,或从小到大、动态地接近那个限制.比如要“一直往前走”才会达到最终的学校南门,发动机“一直开动”才会导致油箱的油量降为最终的0这个限.
对于极限的概念,只需要明白两点:一、它是一个数值或地点;二、要达到这个数值或点,需要动态地逐步靠近并最终接触或相等.
同样的道理,微积分里的极限,也是一个最终的数或地点(你把数轴上的数所对应的点看做地点就行).
数列极限的定义
首先明白什么是数列,数列是如何在实际中产生的,为什么不得不研究它.
简单地讲,数列是一列有序的数.
极限的概念是由求解某些实际问题的精确解答而产生的.例如,用圆的内接正多边形来推算圆的面积时:
内接正六边形面积为$A_1$
内接正十二边形面积为$A_2$
内接正二十四边形面积为$A_3$
如此下去,每次边数加倍,一般地把圆的内接正$6×2^{n-1} $边形的面积记为$A_n (n∈{\bf{N}}^+)$,这样,就得到一列有序的圆内接正多边形的面积:
$$A_1,A_2,A_3,…A_n,...$$它构成了一列有序的数.当$n$越大,内接正多边形与圆的差别就越小,从而以$A_n$作为圆面积的近似值也越精确. 但是无论$n$取得如何大,只要$n$取定了,$A_n$终究只是多边形的面积,而不是圆的面积.因此,设想$n$无限增大(记为$n→∞$,读作$n$趋于无穷大)时,内接正多边形无限接近于圆,同时$A_n$也无限接近于某一确定的数值(确定了半径的圆的真实面积),这个确定的数值就是圆的面积.
上述求圆面积的例子中,我们需要求出$n$趋于无穷大时,正$6×2^{n-1} $边形的面积$A_n$无限接近的某一确定的数值是多少,注意这个符号$“n→∞”$,在这里,我们无法将$n$取无穷大,但是在其它情况中,比如$“x→5”$,$x$有可能取5,也有可能不能取5,比如$\frac{1}{x-5}$中$x→5$($x$趋于5,但是不能等于5).在求圆面积的例子中,$n$无法取无穷大,而我们却需要$n$取无穷大时$A_n$的值,这就只能通过研究$n→∞$时,$A_n$无限接近于哪个确定的数值来获得我们需要的解答.因此,在数学中就出现了专门研究当$n$趋于无穷大时求一列有序的数趋于哪个具体数值的数学内容,也就是现在我们要学习的内容.
再次注意,$x$或$n$趋于某一个数时,比如$x$趋于$x_0(x→x_0)$, $x$可能取$x_0$,也可能不能取$x_0$,这要根据实际的函数解析式来判断,而数学上之所以要研究极限的问题,主要原因还是在于有不能取的情况出现,而能取的情况恰好给了我们求解不能取的情况的办法,怎么运用可以取值的情况来求解不能取值的情况,后面后分析,现在只需要知道有这两种情况.
一个确定了半径的圆有一个面积,这个面积是一个实数,我们的目的就是要求出这个实数.我们把这个实数叫做$n$无限增大,即$n$趋于无穷大时圆的内接正多边形的面积所形成的数列
$$A_1,A_2,A_3,…,A_n,...$$的极限.
由于$n$不断地增大,$A_n$也不断变大,但变大是有极限的,它最大只能达到表示圆的面积的那个数量,设为$A$;$n$ 越大, $A_n$与$A$就越接近,可以无限接近,要多接近有多接近,但是请注意:两者不能相等.之所以不能相等,是因为$n$无法取无穷大,$n$无论多么大,始终是一个数,而无穷大是一个概念,是比任何数都要大的概念,而只有$n$无穷大时,$A_n$才等于圆的面积$A$.
注意,是因为$n$无法取无穷大,才导致$A_n$不可能等于圆的面积$A$.
定义 按照某一法则,对每个$n∈{\bf{N}}^+$,对应着一个确定的实数$x_n$,这些实数$x_n$按照下标$n$从小到大排列得到的一个序列
$$x_1,x_2,x_3,…,x_n,…$$
就叫做数列,简记为\(\{{{x}_{n}}\}\),$x_n$称为数列的一般项或通项.
注意:这里把数列的一般项用大括号括起来表示为集合的形式\(\{{{x}_{n}}\}\),但这只是数列的简记,并不是一个集合,用集合的形式表示数列的元素组成的集合,是.\(\{{{x}_{n}}|{{x}_{n}}=f(n),n\in {{{\bf{N}}}^{+}}\}\).
某一法则是指某种计算方法,比如$\frac{1}{n} + 2$,对于法则$\frac{1}{n} + 2$,对每个$n∈{\bf{N}}^+$,对应着一个确定的实数${x_n} = \frac{1}{n} + 2$,这些实数$x_n$按照下标$n$从小到大排列得到的一个序列
$$3,2.5,2.3,2.25,2.2,...,\frac{1}{n} + 2,...$$就叫做数列,简记为\(\{{{x}_{n}}\}\),$x_n$称为数列的一般项或通项,${x_n} = \frac{1}{n} + 2$
可见,当$n$增大时,这个数列的通项${x_n} = \frac{1}{n} + 2$的值越来越接近2,但是不等于2,之所以不等于2,是因为无论$n$取多么大的数,$\frac{1}{n}$都不等于0,但是我们知道,当$n→∞$时,$\frac{1}{n} \to 0$.注意,无穷大$∞$不是实数,但是比任何实数(无论多么大)都要大.
在几何上,可以将数列的每一项所对应的数依次取数轴上对应的点,构成一列无穷点集.
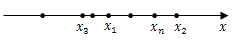
对于我们要讨论的问题来说,重要的是:当$n$无限增大时(即$n→∞$(因为$n∈{\bf{N}}^+$,所以$n→∞$中$∞$指$+∞$)时,对应的$x_n=f(n)$是否能无限接近于某个确定的数值,如果是的话,这个数值等于多少.
我们知道,两个数$a$与$b$之间的接近程度可以用这两个数之差的绝对值$|b-a|$来表示.(在数轴上$|b-a|$表示$a$点与$b$点之间的距离),$|b-a|$越小,$a$与$b$就越接近.
定义 设$\{ {x_n}\} $为一数列,如果存在常数$a$,对于任意给定的正数$ε$(不论它多么小),总存在正整数$N$,使得当$n>N$时,不等式
$$|x_n-a|<ε$$都成立,那么就称常数$a$是数列$\{ {x_n}\} $的极限,或者称数列$\{ {x_n}\} $收敛于$a$,记为
$$x_n→a(n→∞)$$如果不存在这样的常数$a$,就说数列$\{ {x_n}\} $没有极限,或者说数列$\{ {x_n}\} $是发散的,习惯上也说$\mathop {\lim }\limits_{n \to \infty } {x_n}$不存在.
上述定义说明:极限是一个实数,数列的极限是一个实数,当$n$无限增大,趋于无穷大时,数列的通项$x_n$与数列的极限无限接近,但是不相等,不相等的原因在于$n$无法取得无穷大.
收敛是收拢、聚集的意思.
"数列$\{ {x_n}\} $的极限为$a$ "的一个几何解释:
将常数$a$及数列$x_1,x_2,x_3,…,x_n,…$在数轴上用他们的对应点表示出来,再在数轴上做点$a$的$ε$邻域,即开区间$(a-ε,a+ε)$,因不等式$|x_n-a|<ε$与不等式$a - \varepsilon < {x_n} < a + \varepsilon $等价,所以当$n>N$时,所有的点$x_n$都落在开区间$(a-ε,a+ε)$内,相反地,当$n≤N$时,只有有限个(至多只有$N$个)在这区间以外.
$$\mathop {\lim }\limits_{n \to \infty } {x_n} = a \Leftrightarrow \forall \varepsilon > 0,\exists {\bf{N}}^+,当n > N时,|{x_n} - a| < \varepsilon $$
$\forall $表示‘任何’,是英语单词Any的第一个字母A的倒写;
$\exists $表示‘存在’,是英语单词Exit的第一个字母的反写;
n趋于无穷大时,数列$\{ {x_n}\} $的通项$x_n$与它的极限$a$之间无限接近但是不相等,这是因为$n$无法取得无穷大.
