函数的几种性质

函数的有界性

设函数$f(x)$的定义域为$D$，数集$X \subset D$，如果存在数$K_1$，使得

$$f(x)≤K_1$$

对任一$x∈X$都成立，则称函数$f(x)$在$X$上有上界，而$K_1$称为$f(x)$在$X$上的一个上界.如果存在数$K_2$，使得

$$f(x)≥K_2$$

对任一$x∈X$都成立，则称函数$f(x)$在$X$上有下界，而$K_2$称为$f(x)$在$X$上的一个下界. 如果存在正数$M$，使得

$$|f(x)|≤M$$

对任一$x∈X$都成立，则称函数$f(x)$在$X$上有界.如果这样的$M$不存在，就称函数$f(x)$在$X$上无界.

把$|f(x)|≤M$看成$|f(x)-0|≤M$，则$|f(x)|$是$f(x)$的函数值到$y=0$的距离.

函数$f(x)$在$X$上有界的充分必要条件是它在$X$上既有上界又有下界.

符号$“≤”$和“数集$X \subset D$”的注意事项：

(1)函数有界性的定义中，$X$是数集，因此$X$可能是有限数集，比如$X = \left\{ {{x_1},{x_2}} \right\}$或$X = \left\{ {{x_1}} \right\}$；$X$还可能是区间，比如$X=(a,b).$

(2)函数有界性的定义中取的是小于等于或大于等于号$f(x)≤K_1， f(x)≥K_2$和$|f(x)|≤M$，但是取小于、等于和大于号时，有界性也是成立的.比如函数

$$y=2$$

对任一$x \in {\bf{R}}$，有$|f(x)|=2<3=M$，或写为$|f(x)|=2=M$，此时只能取等于号或小于号，但函数$y=2$依然是有界函数；

函数

$$y = \frac{1}{x}$$

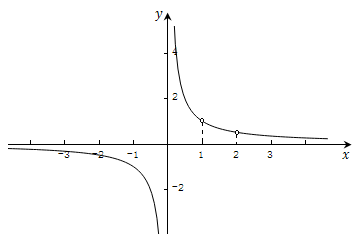
在开区间$X=(1,2)$上，有$|y|=|1/x|<1$，也只能取小于号而不是小于等于号，但该函数区间$X=(1,2)$上依然有上界.

也就是说，在函数的有界性定义中，不一定要使得小于等于或大于等于中的小于和等于以及大于和等于同时成立.

符号“$≤$”指小于或等于，是”$<$”和”$=$”的并集，不需要两者同时成立；实际上， $|f(x)|≤M$等价于$ f(x)| < M$或$f(x)| = M$,满足其中之一或全都满足时，$ |f(x)|≤M$即成立.

函数的单调性

设函数$f(x)$的定义域为$D$，区间$I \subset D$. 如果对于区间$I$上任意两点$x_1$和$x_2$，当${x_1} < {x_2}$时，恒有

$$f({x_1}) < f({x_2})$$

则称函数$f(x)$在区间$I$上是单调增加的；

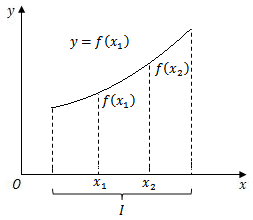
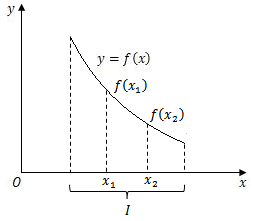
如果对于区间$I$上任意两点$x_1$和$x_2$，当${x_1} < {x_2}$时，恒有

$$f({x_1}) > f({x_2})$$

则称函数$f(x)$在区间$I$上是单调减小的.

单调增加和单调减小函数统称为单调函数.

这里的单调增加是指严格单调增加.不严格的单调增加是：

设函数$f(x)$的定义域为$D$，区间$I \subset D$.

如果对于区间$I$上任意两点$x_1$和$x_2$，当${x_1} < {x_2}$时，恒有

$$f({x_1}) \leqslant f({x_2})$$

则称函数$f(x)$在区间$I$上是单调增加的（不严格的）；

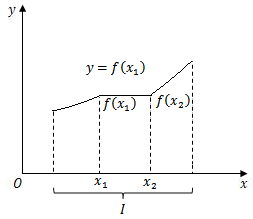
从图像上看，不严格的单调增加函数在整个区间$I$上是增加的，但是中间有水平的部分.因此，所谓严格单调增加，是指在整个单调增加区间内一直增加，不严格单调增加，是指在整个单调增加区间内，有部分是不增加的.

如果对于区间$I$上任一两点$x_1$和$x_2$，当${x_1} < {x_2}$时，恒有

$$f({x_1}) < f({x_2})$$则称函数$f(x)$在区间$I$上是单调减小的.单调减小也有严格和不严格的区分.

函数的奇偶性

设函数$f(x)$的定义域$D$关于原点对称.如果对于任一$x∈D$，

$$f(-x)=f(x)$$

恒成立，则称$f(x)$为偶函数.如果对于任一$x∈D，$

$$f(-x)=-f(x)$$

恒成立，则称$f(x)$为奇函数

对称性

偶函数的图像关于$y$轴对称：$f(-x)=f(x)$

奇函数的图像关于原点对称：$f(-x)=-f(x)$

关于$x$轴对称：由于函数的自变量与因变量之间是一对一或多对一，所以不存在关于$x$轴对称的函数.

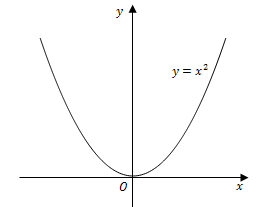
例如，函数$y=x^2$是偶函数，图像关于$y$轴对称.

函数$y=x^3$是奇函数，函数图像关于原点对称.

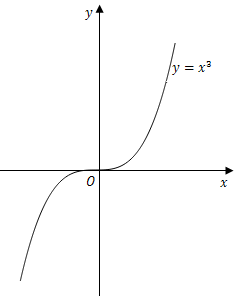
函数的周期性

设函数$f(x)$的定义域为$D$.如果存在一个正数$l$，使得对任一$x∈D$有$(x±l)∈D$，且

$$f(x+l)=f(x)$$

恒成立，则称$f(x)$为周期函数，$l$为$f(x)$的周期，通常我们说周期函数的周期是指最小正周期.

注意：周期函数的定义域为无限集合，但不一定是全体实数.例如正弦函数是周期函数，定义域为全体实数集，正切函数也是周期函数，但是定义域不包括一系列$x = \frac{\pi }{2} + k\pi $处的点，所以它的定义域不是全体实数.