接下来将应用集合和映射的基础知识，给出函数的相关概念.

定义：设数集$D \subset {\bf{R}}$，则称映射

$$f:D \to {\bf{R}}$$

为定义在$D$上的函数，通常记为

$$y = f(x),x \in D$$

这个定义符合前面提到过的函数的定义，即：从实数集（或其子集）$X$到实数集$Y$的映射通常称为定义在$X$上的函数.
自变量：$x$
因变量(因为$x$的变化而跟着变化的量)：$y$
定义域：$D$，记作$D_f$，即$D_f=D$，

之所以用字母$D$表示定义域，是因为$D$是definition的第一个字母.

值域：函数值$f(x)$的全体所构成的集合，记作$R_f$或$f(D)$.

$x$处的函数值记作: $f(x)$即$y=f(x)$.

因变量$y$与自变量$x$之间的这种依赖关系，通常称为函数关系.

表示函数的记号是可以任意取的，比如$y=g(x)，y=F(x)，y=f(x)$等. 在同一个问题中，讨论到几个不同的函数时，为了表示区别，需用不同的记号来表示它们.

函数是从实数集（或其子集）到实数集的映射，如果定义域及对应法则相同，那么由所有函数值构成的值域也相同，所以函数是相同的.

函数的定义域由两种情况来确定：

一种是对有实际背景的函数，根据实际背景中的变量意义来确定.比如表示身高$h$与年龄$t$的函数$h(t)=0.5t$，定义域可能根据实际情况规定为$D = \{ t|0 \leqslant t \leqslant 18\} $.

另一种是对抽象地用算式表达的函数，通常约定这种函数的定义域是使得算式有意义的一切实数组成的集合，这种定义域称为函数的自然定义域.在这种约定下，一般的用算式表达的函数可用$y=f(x)$表达，而不必写出定义域，例如函数

$$y = f(x) = \frac{1}{x}$$

多值函数：从实数集到实数集的一对多的对应法则不是映射，因而也不是函数，比如以点(1,1)为圆心，半径为1的圆的方程$(x-1)^2+(y-1)^2=1$所确定的$y$与$x$的关系在$ 0< x < 2 $时就不是函数关系.从该函数的图像可以看到，在此区间上，同一个$x$值，对应着两个不同的$y$值，这与映射的和函数的定义中需要一对一或多对一的对应法则矛盾.

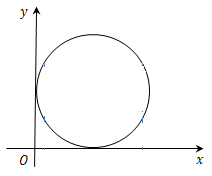
习惯上我们称这种法则[即$(x-1)^2+(y-1)^2=1$]确定了一个多值函数. 给多值函数附加一些条件，可以确定一个映射，即函数，这样的函数称为多值函数的单值分支.例如对于$(x-1)^2+(y-1)^2=1$,若规定$y≥1$，则表示的是上半圆：

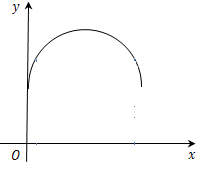
此时一个$x$值，根据对应法则$(x-1)^2+(y-1)^2=1$，只有一个$y$值与之对应.

有时候一个函数由几个不同的对应法则组成，例如 \[y = f(x) = \left\{ \begin{gathered} 2x + 1,x \geqslant 0, \hfill \\ {x^2},x < 0. \hfill \\ \end{gathered} \right.\] 这种在自变量的不同变化范围内，对应法则不同的函数，称为分段函数.

函数的表示方法：解析法（公式法）、图像法和表格法.

函数的图形：用图像法表示函数是基于函数图形的概念，即函数的图形是满足函数解析式的坐标平面上点的集合.

$$\left\{ {P\left( {x,y} \right){\text{|}}y = f\left( x \right),x \in D} \right\}$$

称为函数$y=f(x),x∈D$的图形.$P(x,y)$中的$P$是point的首字母.

几种函数：

常值函数($x$无论取何值，$y$都是常数.)

$$y=3$$

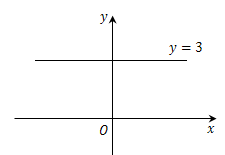
定义域为$D={\bf{R}}$,值域${R_f} = \{ 3\} $.

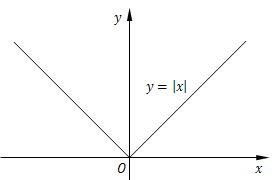
绝对值函数：

\[y = |x| = \left\{ \begin{gathered} {-}x,x < 0, \hfill \\ x,x \geqslant 0 \hfill \\ \end{gathered} \right.\]

取整函数：对任意实数$x$，小于等于$x$的最大整数，记作$[x] $，例如

$$[1.2]=1,[-1]=-1,[-2.5]=-3$$

函数

$$y=[x] $$

称为取整函数，其定义域为${\bf{R}}$,值域$R_f={\bf{Z}}.$

上述三种函数很有用，取整函数在后续数列的地方需要，绝对值函数在函数的连续性与可导性处需要，到时会再提如何运用，现在只需要知道这几种函数不会无缘无故出现在此处即可.