函数的间断点

设函数$f(x)$在点$x_0$的某去心邻域内有定义，如果函数$f(x)$有下列三种情况之一：

(1)在$x=x_0$点没有定义；

(2)在$x=x_0$点有定义，但$\mathop {\lim }\limits_{x \to {x_0}} f(x)$不存在；

(3)在$x=x_0$点有定义，且$\mathop {\lim }\limits_{x \to {x_0}} f(x)$，但$\mathop {\lim }\limits_{x \to {x_0}} f(x) \ne f({x_0}).$

则称函数$f(x)$在点$x_0$不连续，点$x_0$称为函数$f(x)$的不连续点或间断点.

 

函数$y = \tan x$在$x = \frac{\pi }{2}$处没有定义，所以点$x = \frac{\pi }{2}$是函数$y = \tan x$的间断点.因为$\mathop {\lim }\limits_{x \to \frac{\pi }{2}} \tan x = \infty ,$我们称$x = \frac{\pi }{2}$为函数$y = \tan x$的无穷间断点 .

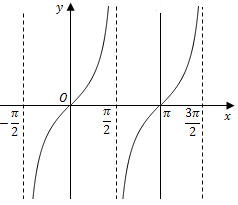
注意：$x$是任意趋近$\frac{\pi }{2}$的，也就是从$\frac{\pi }{2}$的两侧同时趋近，此时的极限$∞$为$+∞$或$-∞$.

 

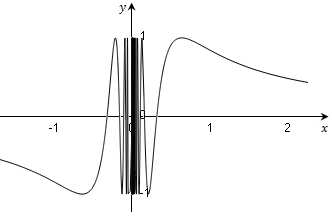
函数$y = \sin \frac{1}{x}$在点$x=0$处没有定义，所以点$x=0$是$y = \sin \frac{1}{x}$的间断点；当$x→0$时，$u = \frac{1}{x} \to \infty ,y = |\sin u|在u = \frac{1}{x} \to \infty $的过程中，函数值在-1和1之间变化无限多次，所以点$x=0$称为函数$y = \sin \frac{1}{x}$的振荡间断点.

 

函数$y = \frac{{3({x^2} - 1)}}{{x - 1}}$在点$x=1$处没有定义，所以点$x=1$是函数的(不连续点)间断点，但是

$$\mathop {\lim }\limits_{x \to 1} \frac{{3({x^2} - 1)}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} 3(x + 1) = 6,$$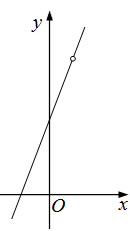

如果补充定义：令$x=1$时，$y=6$，则所给函数在点$x=1$处连续，把$x=1$称为该函数的可去间断(不连续)点.

函数\(f(x) = \left\{ \begin{gathered} x - 2,x<0, \hfill \\ 0,x = 2, \hfill \\ x + 2,x > 0. \hfill \\ \end{gathered} \right.\)

当$x→0$时，

\[\begin{gathered} \mathop {\lim }\limits_{x \to {0^ - }} f(x) = \mathop {\lim }\limits_{x \to {0^ - }} (x - 2) = - 2, \hfill \\ \mathop {\lim }\limits_{x \to {0^ + }} f(x) = \mathop {\lim }\limits_{x \to {0^ + }} (x + 2) = 2. \hfill \\ \end{gathered} \]

左、右极限存在但不相等，因此函数$f(x)$在点$x=0$处的极限不存在.所以点$x=0$是函数的不连续点(间断点).函数图像在点$x=0$处产生了跳跃现象，称点$x=0$为函数的跳跃间断点.

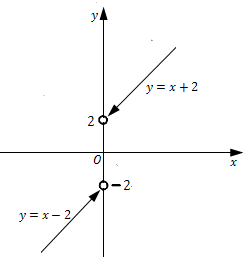
根据函数在点$x_0$处的左右极限是否存在，将间断点分为两类，即第一类间断点和第二类间断点.

第一类：左右极限存在.

左右极限存在且相等 - >可去间断点(可以去掉的间断点，另加定义即可)；

左右极限存在但不相等 - >跳跃间断点

第二类：左右极限不存在.

振荡和无穷间断点(极限趋于无穷不符合极限的定义).