反函数与复合函数

作为逆映射的特例，有以下反函数的概念.

设函数$f:D→f(D)$是单射，则它的逆映射为$f^{-1}:f(D)→D$，称此映射$f^{-1}$为函数$f$的反函数. 按此定义，对于每个$y∈f(D)$，有唯一的$x∈D$，使得$f(x)=y$，于是有

$$f^{-1} (y)=x$$

这就是说，反函数$f^{-1}$的对应法则是完全由函数$f$所确定的.

例如，函数$y=x^3$是单射，它的反函数是$x = \root 3 \of y $很显然，反函数的对应法则$x = \root 3 \of y $完全由函数$y=x^3$确定.

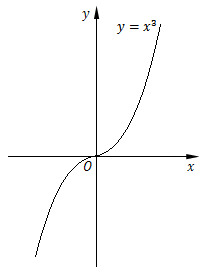
习惯上，我们用$y$表示因变量，$x$表示自变量，因此$y=x^3$的反函数$x = \root 3 \of y $写为$y = \root 3 \of x $，相应的图像为：

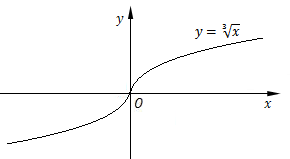
将函数$y=x^3$和它的反函数$y = \root 3 \of x $的图像画在同一坐标系中，我们发现，两者的图像关于直线$y=x$对称.

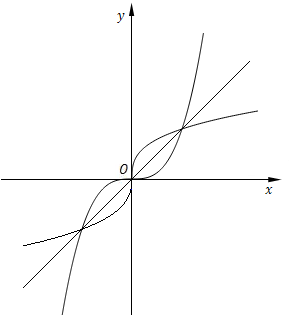
注意：前面我们讲到逆映射时，有两种映射存在逆映射：

单射：$\forall f:X \to Y\left( {{x_1} \ne {x_2},f\left( {{x_1}} \right) \ne f\left( {{x_2}} \right)} \right),\exists {f^{ - 1}}:{R_f} \to X.$

单射的逆映射是从单射的值域$R_f$到定义域的新映射，不是从单射值域的范围Y到定义域.

一一映射：$\forall f:X \to Y\left( {{x_1} \ne {x_2},f\left( {{x_1}} \right) \ne f\left( {{x_2}} \right),\forall y \in {R_f},\exists x \in X} \right),\exists {f^{ - 1}}:Y \to X.$

一一映射的逆映射是从一一映射值域的范围$Y$到定义域$X$的新映射.

在这里定义逆函数时，我们用到的条件是从单射到逆映射，符合逆映射的第1种情况.

注意值域的范围$Y$与值域$R_f$的区别.

原函数与其逆函数具有相同的单调性.

把原来的函数称为直接函数，直接函数与逆函数的图像关于$y=x$轴对称.

关于$y=x$轴对称的点的坐标：点$Q(a,b)$关于直线$y=x$对称的点的坐标为$P(b,a)$

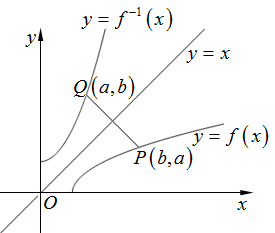
复合函数

复合函数是复合映射的一种特列，按照通常函数的记号，复合函数的概念可如下表述.

设函数$y=f(u)$的定义域为$D_f$，函数$u=g(x)$的定义域为$D_g$，且其值域${R_g} \subset {D_f}$ .则由下式确定的函数

$$y=f[g(x)],x∈D_g.$$

称为由函数函数$u=g(x)$与函数$y=f(u)$构成的复合函数，它的定义域为$D_g$，$u$变量称为中间变量.通常记为

$$({f^o}g)(x) = f[g(x)]$$

为了简便起见，在用数学表达式表示函数时，不再写出定义域的范围，其定义域是满足该复合函数的自然定义域.

例如函数$y = {\bf{sin}} (2x+1)$是由函数$y = {\bf{sin}} u$,$u=2x+1$复合而成.

函数的运算

设函数$f(x)，g(x)$的定义域依次为${D_1},{D_2},D = {D_1} \cap {D_2} \ne $Ø,则我们可以定义这两个函数的下列运算：

和差：$f±g:(f±g)(x)=f(x)±g(x),x∈D$；

积：$f \cdot g:(f \cdot g)(x) = f(x) \cdot g(x),x \in D$;

商：$\frac{f}{g}:(\frac{f}{g})(x) = \frac{{f(x)}}{{g(x)}},x \in D\backslash \{ x|g(x) = 0,x \in D\} $

注意：${D_1} \cap {D_2} \ne $Ø是保证两个函数在上述运算时同时成立的条件，不可缺少.有时候会认为集合$\{ x|g(x) = 0,x \in D\} $中$x$应该是$x∈D_2$.实际上,在$(\frac{f}{g})(x) = \frac{{f(x)}}{{g(x)}}$中,$x \in D$,此时只需要将满足$x∈D$且使$g(x)=0$的$x$去掉,因此,$\{ x|g(x) = 0,x \in D\} $ 中$x∈D$是正确的.函数的运算是一个定义，不需要证明.或者说，函数的上述运算，实质上都是实数之间的加减乘除运算，要证明它们，显然就是证明为什么1+1=2的问题了.