如果函数在某一点的极限等于函数在该点的函数值，那么就说函数在该点连续；如果函数$f(x)$在开区间$(a,b)$内连续，在右端点左连续，在左端点右连续，那么函数$f(x)$就是在闭区间$[a,b]$上连续的.

在闭区间上连续的函数有几个重要的性质.

有界性与最大值最小值定理

在区间$I$上有定义的函数$f(x)$，如果有$x_0∈I$，使得对于任一$x∈I$，都有

$$f(x)≤f(x_0 ) (f(x)≥f(x_0 ))$$

则称$f(x_0 )$是函数$f(x)$在区间$I$上的最大值(最小值).

对于某一区间，在不需要辨明所论区间是否包含端点的场合，我们就简单地称它为“区间”，且常用$I$表示.因此，上面的区间可能指开区间、闭区间、半开半闭区间中的任意一种.

简单地讲，区间$I$上某一点的函数值$f(x_0 )$是函数在该区间上的最大值或最小值.

例如，函数$f(x) = 1 + \cos x$且有$x_0=0∈[-π,π]$，使得对于任一$x∈[-π,π]$，都有$f(x)≤f(x_0 )=f(0)=2$，所以$f(0)$是函数$f(x) = 1 + \cos x$在区间$[-π,π]$上的最大值，函数$f(x)=\sin x$在区间$(-\infty ,+ \infty)$内有最大值1和最小值-1.

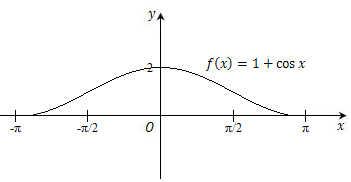
$f(x)=x$在开区间$(a,b)$内既无最大值又无最小值.

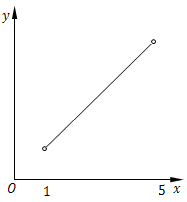
此外，最大值和最小值可以相等.例如常值函数$f(x)=2$在闭区间$[1,5]$上的最大值和最小值都是2.

定理1（有界性与最大值最小值定理）在闭区间上连续的函数在该区间上有界且一定能取得它的最大值和最小值.

在闭区间内有间断点，或在开区间内连续以及在开区间内有间断点的函数，不一定有界或能取得它的最大值和最小值.

例 在闭区间内有间断点的函数没有最大值和最小值

\[y = f(x) = \left\{ \begin{gathered} - x + 1,0 \leqslant x < 1, \hfill \\ 1,x = 1, \hfill \\ - x + 3,1 < x \leqslant 2. \hfill \\ \end{gathered} \right.\]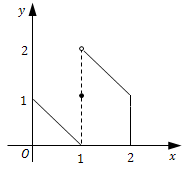

例 在开区间内连续的函数无界且没有最大值和最小值

\[y = \tan x,x \in ( - \frac{\pi }{2},\frac{\pi }{2})\]

另外，对于函数$f(x)=x$，在开区间$(1,5)$上，由于函数无法取$x=5$，因此在开区间$(1,5)$上函数$f(x)=x$无最大值.

零点定理与介值定理

若$x_0$使$f(x_0 )=0$，那么$x_0$称为函数$f(x)$的零点.

定理2（零点定理） 设函数$f(x)$在闭区间$[a,b]$上连续，且$f(a)$与$f(b)$异号（即$f(a) \cdot f(b) < 0$），那么在开区间$(a,b)$内至少有一点$ξ$，使得

$$f(ξ)=0$$

注意，“那么在开区间$(a,b)$内至少有一点$ξ$”，这句话意味着$ξ≠a,b$，因为闭区间的端点$a,b$异号，一个为正，另一个为负，不可能是0，所以要去除端点，从而在开区间$(a,b)$内.

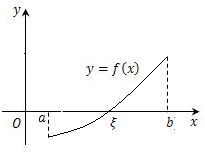
定理3 (介值定理) 设函数$f(x)$在闭区间$[a,b]$上连续，且在这区间的端点取不同的函数值$f(a)=A$及$f(b)=B$，那么，对于$A$与$B$之间的任意一个数$C$，在开区间$(a,b)$内至少有一点$ξ$，使得$f(\xi ) = C(a < \xi < b).$

证明:已知$A < C < B或B < C < A,$

当$A < C < B$时，$A-C < 0,B-C > 0$，设函数$φ(x)=f(x)-C$，因为$f(x)$在闭区间$[a,b]$上连续，根据连续函数的和、差、积、商的连续性，$φ(x)=f(x)-C$在闭区间$[a,b]$上也连续.根据定理2，在开区间$(a,b)$内至少有一点$ξ$，使得

$$φ(ξ)=f(ξ)-C=0(a < ξ < b)$$ $$f(ξ)=C(a < ξ < b)$$

推论 在闭区间上连续的函数必取得介于最大值M与最小值m之间的任何值.

因为$M≠m$，设$f(x_1 )=m,f(x_2 )=M$，在闭区间$[x_1,x_2 ]$(或$[x_2,x_1 ])$上应用定理3即得上述推论.

 

一致连续性

在区间$I$上连续的函数$f(x)$，当$x_0∈I$时，根据连续函数的定义，$\forall \varepsilon > 0,\exists \delta > 0,当|x - {x_0}| < \delta ,有|f(x) - f({x_0})| < \varepsilon .$

通常这个$δ$不但和$ε$有关，而且还与$x_0$有关，即相同的$ε$，不同的$x_0$，这个$δ$就不一定相同.可是对于某些函数，却存在着只与$ε$有关，而对区间$I$上任何点$x_0$都能适用的$δ$，我们称这样的函数在区间$I$上一致连续.

定义 设函数$f(x)$在区间$I$上有定义.如果对于任意给定的正数$ε$，总存在着正数$δ$，使得对于区间$I$上的任意两点$x_1,x_2$，当$|x_1-x_2 |<δ$时，就有 $$|f(x_1 )-f(x_2 )|<ε$$ 那么称函数$f(x)$在区间$I$上是一致连续的.

充分性证明：

$$\eqalign{ & \forall \frac{\varepsilon }{2} > 0,\exists {\delta _1} > 0,当|x - {x_1}| < {\delta _1}时,有|f(x) - f({x_1})| < \frac{\varepsilon }{2}, \cr & \forall \frac{\varepsilon }{2} > 0,\exists {\delta _2} > 0,当|x - {x_2}| < {\delta _2}时,有|f(x) - f({x_2})| < \frac{\varepsilon }{2}, \cr} $$

取$\delta = \min \{ {\delta _1},{\delta _2}\} ,\forall \frac{\varepsilon }{2} > 0,\exists \delta > 0,$当

$$\eqalign{ & |x - {x_1}| < \frac{\delta }{2}时,有|f(x) - f({x_1})| < \frac{\varepsilon }{2}, \cr & |x - {x_2}| < \frac{\delta }{2}时,有|f({x_2}) - f(x)| < \frac{\varepsilon }{2}, \cr} $$

那么，

$$|x_2-x_1 |≤|x-x_1 |+|x-x_2|<δ时，有 |f(x_1 )-f(x_2 )|<ε.$$

另一种证明思路是：因为$x_1$和$x_2$都是任意的，当任意的$x_1$取定以后，$x_2$就成为$x_1$附近任意一点，利用函数的连续性定义就可以得到证明.

上面的定义是函数一致连续性概念的数学语言表述，看似与概念不一致，实际上，因为在闭区间上连续的函数在该区间上也一致连续，所以很容易举出例子从定义推导概念，或从概念推导定义，从而印证一致连续性的定义与概念是一致的（定义符合概念，概念也符合定义）.

例 $f(x)=2x-1$

该函数是初等函数，初等函数在定义区间上是连续函数，我们在闭区间$[0,5]$内讨论.该函数符合一致连续性的概念吗？换句话说，相同的$ε$，不同的$x_0，δ$会相同吗？设$x_0$是闭区间$[0,5]$上的任意一点，因为$f(x)=2x-1$在该区间上连续，$\forall \varepsilon > 0,$

$$|2x-1-(2x_0-1)|=2|x-x_0 |$$

设$\delta = \frac{\varepsilon }{2},当|x - {x_0}| < \delta = \frac{\varepsilon }{2}时,|2x - 1 - (2{x_0} - 1)| = 2|x - {x_0}| < \varepsilon ,$

也就是说，当$x$取闭区间$[0,5]$上的任意值时，相同的$ε$，不同的$x_0，δ$也相同，这就是函数一致连续的概念.

从定义上看，只需将上面的$x$换成任意一点$x_1$即得定义的表达式，说明该函数也符合一致连续的定义.

闭区间内连续的函数都是一致连续的.