函数的极限

函数极限的性质和有极限的函数的性质

前面介绍了数列极限的性质，而数列是一种特殊的函数(特殊性表现在数列的定义域是自然数集，是离散的)，与收敛数列（$n→+∞$时极限存在的数列）的性质相比较，可得函数极限的以及有极限的函数的一些相应的性质.

若函数有极限，即$\mathop {\lim }\limits_{x \to {x_0}} f(x) = A$,则称函数$f(x)$在$x_0$点收敛.

定理1(函数极限的唯一性)如果$\mathop {\lim }\limits_{x \to {x_0}} f(x) = A$存在，那么这个极限是唯一的.

定理2(有极限的函数的局部有界性) 如果$\mathop {\lim }\limits_{x \to {x_0}} f(x) = A$,那么存在常数$M>0$和$δ>0$，使得$0<|x-x_0 |<δ$ 时，有$|f(x)|≤M$.

证明：因为

$$\mathop {\lim }\limits_{x \to {x_0}} f(x) = A$$

取$ε=1$，$\exists δ>0$，当$0<|x-x_0 |<δ$ 时，有$$|f(x)-A|<1\Rightarrow |f(x)|=|f(x)-A+A|≤|f(x)-A|+|A|<1+|A|$$

记$M=1+|A|$，则定理2得证.

定理3 (有极限的函数的局部保号性)如果$\mathop {\lim }\limits_{x \to {x_0}} f(x) = A$，且$A>0$(或$A<0$)，那么存在常数$δ>0$,使得当$0<|x-x_0 |<δ$ 时,有$f(x)>0$(或$f(x)<0).$

证明：取$\varepsilon = \frac{A}{2} > 0$或$\varepsilon = -\frac{A}{2} > 0$，利用函数极限的定义可以得到证明.

取$\varepsilon = \frac{A}{2} > 0$，

则$\exists δ>0$，当$0<|x-x_0 |<δ$时，有

$$|f(x) - A| < \frac{A}{2} \Rightarrow - \frac{A}{2} < f(x) - A < \frac{A}{2} \Rightarrow 0 < \frac{A}{2} < f(x) < \frac{{3A}}{2}$$

取$\varepsilon =- \frac{A}{2} > 0$，

则$\exists δ>0$，当$0<|x-x_0 |<δ$时，有

$$|f(x) - A| < -\frac{A}{2} \Rightarrow \frac{A}{2} < f(x) - A < -\frac{A}{2} \Rightarrow \frac{3A}{2} < f(x) < \frac{{A}}{2}<0$$

定理3' 如果$\mathop {\lim }\limits_{x \to {x_0}} f(x) = A（A≠0）$，那么存在$x_0$的某一去心邻域$\mathop U\limits^0 \left( {x_0 } \right) $，当$x∈\mathop U\limits^0 \left( {x_0} \right) $时，有

$$|f(x)| > \frac{{|A|}}{2}$$

证明：根据定理3的结论，

当$A>0$时，$\frac{A}{2} < f(x) < \frac{{3A}}{2},$

当$A<0$时，$\frac{3A}{2} < f(x) < \frac{{A}}{2},$

那么，当$A≠0$时，就有

$|f(x)| > \frac{{|A|}}{2}$，准确地说，是

$$\frac{{|A|}}{2}<|f(x)| < \frac{{|3A|}}{2}$$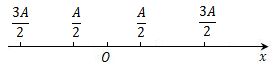

推论 如果在$x_0$的某去心邻域内$f(x)≥0$或$(f(x)≤0)$，且

$$\mathop {\lim }\limits_{x \to {x_0}} f(x) = A$$

，那么$A≥0$(或$A≤0$).

定理4（函数极限与数列极限的关系）如果极限$\mathop {\lim }\limits_{x \to {x_0}} f(x)$存在，$\{ {x_n}\} $为函数$f(x)$的定义域内任一收敛于$x_0$的数列，且满足$x_n≠x_0 (n∈{\bf{N}}^+)$，那么相应的函数值数列$f(x_n)$必收敛，且$\mathop {\lim }\limits_{n \to \infty } f({x_n}) = \mathop {\lim }\limits_{x \to {x_0}} f(x).$

证明：设$\mathop {\lim }\limits_{x \to {x_0}} f(x) = A$，则$\forall \varepsilon > 0,\exists \delta > 0,$当$0<|x-x_0 |<δ$时，有$|f(x)-A|<ε,$又因为$\{ {x_n}\} $为函数$f(x)$的定义域内任一收敛于$x_0$的数列，所以$\mathop {\lim }\limits_{n \to \infty } {x_n} = {x_0}$，故对$\delta > 0,\exists \ N,$当$n>N$时，有$|x_n-x_0 |<δ.$

又因为$x_n≠x_0 (n∈\text{N}^+)$，所以当$n>N$时，有$0<|x_n-x_0 |<δ$，从而$|f(x_n )-A|<ε$，即

$$\mathop {\lim }\limits_{x \to \infty } f({x_n}) = A $$

所以

$$\mathop {\lim }\limits_{n \to \infty } f({x_n}) = \mathop {\lim }\limits_{x \to {x_0}} f(x)$$