曲率及其计算公式

曲率是以数量的形式描述曲线的弯曲程度的一个概念.

曲线的弯曲程度不仅和曲线上点$M_1$移动到点$M_2$时两点处切线的转角大小有关，而且还与曲线弧段的长度$|\widehat {{M_1}{M_2}}|$有关.

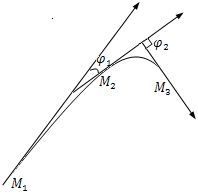
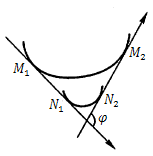
设曲线$C$是光滑的（每点都有切线，且切线随切点的移动而连续移动.），在曲线$C$上选定一点$M_0$作为度量弧$s$的基点.设曲线上点$M$对应于弧$s$，在点$M$处切线的倾角为$α$（这里假定曲线$C$所在的平面上已经设立了$xOy$坐标系），曲线上另外一点$M'$对应于弧$s + \Delta s$，在点$M'$处切线的倾角为$α + \Delta α$，那么弧段$\widehat {MM'}$的长度为$|\Delta s|$，当动点从$M$移动到$M'$时切线转过的角度为$|\Delta α|$

注意，这里使用弧段的长度和切线转过的角度的大小，不考虑正负.

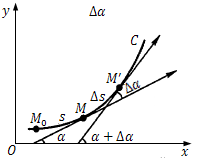
我们用比值$\frac{{|\Delta \alpha |}}{{|\Delta s|}}$，即单位弧段上切线转过的角度的大小来表达弧段$\widehat {MM'}$的平均弯曲程度，把这个比值叫做弧段$\widehat {MM'}$的平均曲率，记为$\overline K $.

$$\overline K = \frac{{|\Delta \alpha |}}{{|\Delta s|}}$$

有一个疑问：曲率的定义为什么不是转过的单位角度对应的弧长?

原因在于我们研究的是曲线的弯曲程度，因此是在单位弧段上，或者说，最初看弯曲程度时，是考察转过的角度大小，角度大则弯曲程度大，后来发现弯曲程度还与弧长有关，于是查看在转过相同弧长时的角度大小.

当$\Delta s \to 0$时（即$M'→M$），上述平均曲率的极限叫做曲线$C$在点$M$处的曲率，记作$K$，即

$$K = \mathop {\lim }\limits_{\Delta s \to 0} \frac{{|\Delta \alpha |}}{{|\Delta s|}}$$

在$\mathop {\lim }\limits_{\Delta s \to 0} \frac{{|\Delta \alpha |}}{{|\Delta s|}} = \frac{{{\text{d}}\alpha }}{{{\text{d}}s}}$存在的条件下，$K$也可以表示为

$$K = |\frac{{{\text{d}}\alpha }}{{{\text{d}}s}}|$$

对于直线，$K=0$.

对于半径为$a$的圆，

$${\angle}MDM' = \frac{{\Delta s}}{a}$$ $$\frac{{\Delta \alpha }}{{\Delta s}} = \frac{{\frac{{\Delta s}}{a}}}{{\Delta s}} = \frac{1}{a}$$

从而

$$K = \left| {\frac{{{\text{d}}\alpha }}{{{\text{d}}s}}} \right| = \frac{1}{a}$$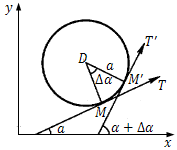

直线的曲率为0；圆的曲率是半径的倒数，半径越大，曲率越小，圆周的弯曲程度越小.因此曲率的大小表示曲线的弯曲程度，曲率越大，曲线越弯曲.

现在来导出一般情况下曲率的计算公式.

设曲线的直角坐标方程是$y=f(x)$，且具有二阶导数（这时$f'(x)$连续，从而曲线是光滑的）.因为$\tan \alpha = y'$，所以

$${\sec ^2}\alpha \frac{{{\text{d}}\alpha }}{{{\text{d}}x}} = y''$$ $$\frac{{{\text{d}}\alpha }}{{{\text{d}}x}} = \frac{{y''}}{{{{\sec }^2}\alpha }} = \frac{{y''}}{{1 + {{\tan }^2}\alpha }} = \frac{{y''}}{{1 + y{'^2}}}$$ $${\text{d}}\alpha = \frac{{y''}}{{1 + y{'^2}}}{\text{d}}x$$

又因为${\text{d}}s = \sqrt {1 + y{'^2}} {\text{d}}x$，根据曲率的公式

$$K = \left| {\frac{{{\text{d}}\alpha }}{{{\text{d}}s}}} \right|$$

得到

\[K = \left| {\frac{{{\mathbf{d}}\alpha }}{{{\mathbf{d}}s}}} \right| = |\frac{{\frac{{{y{''}}}}{{1 + {y'}^2}}{\mathbf{d}}x}}{{\sqrt {1 + {y'}^2} {\mathbf{d}}x}}| = \frac{{|{y{''}}|}}{{\sqrt[2]{{{{(1 + {y'}^2)}^3}}}}}\]

设曲线的参数方程为

\[\left\{ {\begin{array}{*{20}{c}} {x = \varphi (t),} \\ {y = \gamma (t),} \end{array}} \right.\] \[\begin{gathered} y' = \frac{{\gamma '(t)}}{{\varphi '(t)}} \hfill \\ y'' = \frac{{\gamma ''\left( t \right)\varphi '\left( t \right) - \gamma '(t)\varphi ''(t)}}{{\varphi {'^2}(t)}} \hfill \\ \end{gathered} \]

则

$$K = \left| {\frac{{\frac{{\gamma ''\left( t \right)\varphi '\left( t \right) - \gamma '\left( t \right)\varphi ''\left( t \right)}}{{{\varphi ^{'2}}\left( t \right)}}}}{{\root 2 \of {{{\left[ {1 + \frac{{{{\gamma '}^2}\left( t \right)}}{{{{\varphi '}^2}\left( t \right)}}} \right]}^3}} }}} \right| = \frac{{\left| {\gamma ''\left( t \right)\varphi '\left( t \right) - \gamma '\left( t \right)\varphi ''\left( t \right)} \right|}}{{\root 2 \of {{{\left[ {{{\varphi '}^2}\left( t \right) + {{\gamma '}^2}\left( t \right)} \right]}^3}} }}$$

在有些实际问题中，$y'$与1比较起来是很小的，此时有曲率的近似计算公式

\[K \approx |y''|\]

曲率圆与曲率半径

设曲线$y=f(x)$在点$M(x,y)$处的曲率为$K(K≠0)$.在点$M$处的曲线的法线上，在凹的一侧取点$D$，使$|DM|=1/K$，以$|DM|=1/K=ρ$为半径，$D$为圆心作圆，这个圆叫做曲线在点$M$处的曲率圆，$D$叫做曲线在点$M$处的曲率中心，$ρ$叫做曲线在点$M$处的曲率半径.

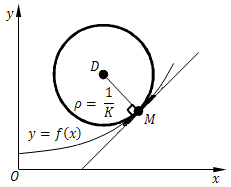
在实际问题中，经常用曲率圆在点$M$邻近的一段圆弧来近似代替曲线弧，以使问题简化.