最大值最小值问题

假设函数$f(x)$在闭区间$[a,b]$上连续，在开区间$(a,b)$内除了有限个点外可导，且至多有有限个驻点.在上述条件下，我们来讨论$f(x)$在$[a,b]$上的最大值和最小值的求法.

如图为在闭区间$[a,b]$上连续，在开区间$(a,b)$内除了有限个点外可导，有无限多个驻点的情况.

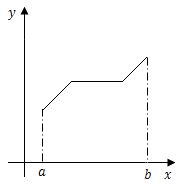
由闭区间上连续函数的性质，可知$f(x)$在$[a,b]$上的最大值最小值一定存在.

其次，如果最大值或最小值$f(x_0 )$在开区间$(a,b)$内的点$x_0$处取得，在$(a,b)$内有$f(x)≤f(x_0 )$或$f(x)≥f(x_0 )$ ，由于$f(x_0 )$是最大值或最小值，所以去掉$x_0$后，有$f(x) < f(x_0 )$或$f(x) > f(x_0 )$，也就是说，$x_0$是极值点.因为$f(x)$在$(a,b)$内除有限个点外可导，由费马引理可知，$f'(x_0 )=0$或不存在，即$x_0$一定是$f(x)$的驻点或不可导点.

假设“至多有有限个驻点”的目的是：如果有无穷个驻点，那么我们需要计算无穷次驻点的函数值，那就算不完了，这在实际应用中是不可取的.

因此，可用如下方法求$f(x)$在$[a,b]$上的最大值和最小值.

(1)求出$f(x)$在$(a,b)$内的驻点及不可导点（求出导函数后判断自变量使导函数不存在的点）

(2)计算驻点、不可导点和区间端点的函数值.

(3)比较(2)中诸值的大小，其中最大值便是$f(x)$在$[a,b]$上的最大值，最小值便是$f(x)$在$[a,b]$上的最小值.