柯西中值定理

如果函数$f(x)$及$F(x)$满足

（1）在闭区间$[a,b]$上连续；

（2）在开区间$(a,b)$内可导；

（3）对任一$x∈(a,b)，F'(x)≠0$，

那么在$(a,b)$内至少有一点$ξ$，使等式

$$\frac{{f\left( b \right) - f(a)}}{{F\left( b \right) - F(a)}} = \frac{{f'(\xi )}}{{F'(\xi )}}$$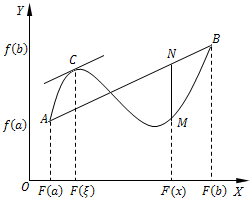

证明：将拉格朗日中值定理中的函数$f(x)$用参数方程所确定的函数

\[\left\{ {\begin{array}{*{20}{c}} {X = F(x),} \\ {Y = f(x),} \end{array}(a \leqslant x \leqslant b)} \right.\]

代替，其中参数是$x$.参数方程中用$f(x)$表示$y$的原因在于通常情况下我们用$f(x)$来表示函数关系中的因变量.

对$F(x)$应用拉格朗日中值定理，得：

\[F\left( b \right) - F\left( a \right) = F'\left( \eta \right)\left( {b - a} \right),(a < \eta < b)\]

根据假定，$F'\left( \eta \right) \ne 0$，又$b - a \ne 0$，所以$F\left( b \right) - F\left( a \right) \ne 0.$

类似拉格朗日中值定理的证明，仍然以表示有向线段$NM$的值的函数$φ(x)$作为辅助函数，设直线$AB$的方程为$y=L(x)$，则

$$L\left( x \right) = f\left( a \right) + \frac{{f\left( b \right) - f\left( a \right)}}{{F\left( b \right) - F(a)}}[F\left( x \right) - F(a)]$$

由于点$M、N$的纵坐标依次为$f(x)$和$L(x)$，因此表示有向线段$NM$的值的函数

$$\varphi \left( x \right) = f\left( x \right) - L\left( x \right) = f\left( x \right) - f(a) - \frac{{f\left( b \right) - f\left( a \right)}}{{F\left( b \right) - F(a)}}[F\left( x \right) - F(a)]$$

$φ(x)$在闭区间$[a,b]$上连续、在开区间$(a,b)$内可导的分析参考罗尔定理的证明. 对$φ(x)$应用罗尔定理得：

$$\varphi '\left( \xi \right) = f'\left( \xi \right) - \frac{{f\left( b \right) - f\left( a \right)}}{{F\left( b \right) - F\left( a \right)}} \cdot F'\left( \xi \right) = 0$$

即

$$\frac{{f\left( b \right) - f\left( a \right)}}{{F\left( b \right) - F\left( a \right)}} = \frac{{f'\left( \xi \right)}}{{F'\left( \xi \right)}}$$

用参数方程所确定的函数代替曲线函数，在参数方程中，仍然用习惯上使用的$f(x)$表示参数方程中的$Y$，这是记忆柯西中值定理的方法，也是柯西中值定理的实质.