弧微分

设函数$f(x)$在开区间$(a,b)$内具有连续导数.

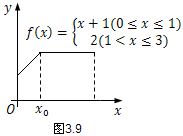
连续导数：如果导数（导函数）不连续（间断），比如，（1）导函数在某点$x_0$处的左右极限，即左右导数存在但不相等；（2）不可导（导数为无穷大）（例如$y = {x^{\frac{1}{3}}}$在$x_0=0$处）.

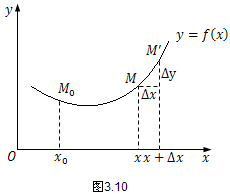
在曲线$y=f(x)$上取固定点$M_0 (x_0,y_0)$作为度量弧长的基点，并规定依$x$增大的方向作为曲线的正方向.对曲线上任一点$M(x,y)$，规定有向弧段$\widehat {{M_0}M}$的值$s$(简称为弧$s$)如下：$|s|$等于弧段的长度，

$s > 0$时，有向弧段$\widehat {{M_0}M}$的方向与曲线的正方向一致，

$s < 0$时，有向弧段$\widehat {{M_0}M}$的方向与曲线的正方向相反.

显然，弧s（有向弧段($\widehat {{M_0}M}$的值$s$）与$x$存在函数关系：$s=s(x)$，而且$s(x)$是$x$的单调增加函数.

总结：我们规定了

有向曲线：$y=f(x)$

有向弧段$\widehat {{M_0}M}$：$\widehat {{M_0}M}$

有向弧段$\widehat {{M_0}M}$的值：$\widehat {{M_0}M}$或$s$

有向弧段$\widehat {{M_0}M}$的长度：$|s|$

$\widehat {{M_0}M}$既表示有向弧段，又表示有向弧段的值$s$

下面来求$s(x)$的导数和微分.

设$x,x + \Delta x$为$(a,b)$内两个邻近的点，它们在曲线$y=f(x)$上的对应点为$M,M'$，并设对应于$x$的增量为$\Delta x$，弧s的增量为$\Delta s$，那么

$$\Delta s = \widehat {{M_0}M'} - \widehat {{M_0}M} = \widehat {MM'}$$

用$|MM' |$表示$M,M'$之间的弦长，

$$\eqalign{ & {\left( {\frac{{\Delta s}}{{\Delta x}}} \right)^2} = {\left( {\frac{{\widehat {MM'}}}{{\Delta x}}} \right)^2} = {\left( {\frac{{\widehat {MM'}}}{{\left| {MM'} \right|}}} \right)^2}\cdot\frac{{{{\left| {MM'} \right|}^2}}}{{{{\left( {\Delta x} \right)}^2}}} \cr & = {\left( {\frac{{\widehat {MM'}}}{{\left| {MM'} \right|}}} \right)^2}\cdot\frac{{{{\left( {\Delta x} \right)}^2} + {{\left( {\Delta y} \right)}^2}}}{{{{\left( {\Delta x} \right)}^2}}} \cr & = {\left( {\frac{{\widehat {MM'}}}{{\left| {MM'} \right|}}} \right)^2}\left[ {1 + {{\left( {\frac{{\Delta y}}{{\Delta x}}} \right)}^2}} \right] \cr & \frac{{\Delta s}}{{\Delta x}} = \pm \sqrt {{{\left( {\frac{{\widehat {MM'}}}{{\left| {MM'} \right|}}} \right)}^2}\cdot\left[ {1 + {{\left( {\frac{{\Delta y}}{{\Delta x}}} \right)}^2}} \right]} \cr} $$

令$\Delta x \to 0$取极限，此时$M'→M$，那么弧的长度与弦的长度之比的极限等于1，即

$$\mathop {\lim }\limits_{M' \to M} \frac{{\widehat {|MM'|}}}{{\left| {MM'} \right|}} = 1$$

注意，我们在公式中一直使用有向弧段$\widehat {{M_0}M}$的值：$\widehat {{M_0}M}$，此处之所以用弧的长度与弦的长度之比，是因为有二次方，使得有向弧段$\widehat {{M_0}M}$的值$\widehat {{M_0}M}$（可能正可能负）二次方之后都为正.

又

$$\mathop {\lim }\limits_{\Delta x \to 0} \frac{{\Delta y}}{{\Delta x}} = y'$$

所以

$$\frac{{{\text{d}}s}}{{{\text{d}}x}} = \pm \sqrt {1 + y{'^2}} $$

由于$s=s(x)$是单调增加函数，从而根号前应取正号，于是有

$${\bf{d}}s = \sqrt {1 + y{'^2}} {\bf{d}}x$$

这就是弧微分公式.

由于推导中用到曲线$y=f(x)$的导数$y'$，因此最开始要求曲线的导数存在，且连续（因为后面要求$s$，此时要求${\bf{d}}s = \sqrt {1 + y{'^2}} {\bf{d}}x$中的被积表达式连续（不定积分时会讲到））.