微分中值定理
洛必达法则
泰勒公式
函数的单调性与曲线的凹凸性
函数的极值与最大值和最小值
曲率
泰勒定理是微积分学的基础知识和数学分析的主要工具之一,在理工科教材中作为其他学科的辅助工具来讲解,其中对于用代数多项式函数${P_n}(x)$近似代替函数$f(x)$的原因以及${P_n}(x)$的解析式的形式讲解不充分;泰勒(1685-1731)生活在柯西(1789-1857)出生前,显然他不可能以柯西中值定理为基础来证明余项${R_n}(x)$,这两个疑问促使作者去寻求多项式函数${P_n}(x)$的由来以及泰勒发现泰勒定理的过程.
一般地,如果给定一个数列
$${u_1},{u_2},{u_3},...,{u_n},...$$则由这数列构成的表达式
$${u_1} + {u_2} + {u_3} + \ldots + {u_n} + \ldots $$叫做(常数项/函数项)无穷级数,简称级数,记为$\sum\limits_{n = 1}^\infty {{u_n}} $,即
$$\mathop \sum \limits_{n = 1}^\infty {u_n} = {u_1} + {u_2} + {u_3} + \ldots + {u_n} + \ldots $$其中第$n$项${u_n}$叫做级数的一般项.
定义 如果级数$\mathop \sum \limits_{n = 1}^\infty {u_n}$的部分和数列$\{ {s_n}\} $有极限$s$,即
$$\mathop {\lim }\limits_{n \to \infty } {s_n} = s$$则称无穷级数$\mathop \sum \limits_{n = 1}^\infty {u_n}$收敛,这时的$s$叫做这级数的和,并写成
$$s = {u_1} + {u_2} + {u_3} + \ldots + {u_n} + \ldots $$如果$\{ {s_n}\} $没有极限,则称无穷级数$\mathop \sum \limits_{n = 1}^\infty {u_n}$发散.
无穷级数
$$\mathop \sum \limits_{n = 0}^\infty a{q^n} = a + aq + a{q^2} + \ldots + a{q^n} + \ldots {\text{}}(1)$$叫做等比级数(又称为几何级数),其中$a≠0,q$叫做级数的公比.
如果$q≠1$,则
$$\eqalign{ & {s_n} = a + aq + a{q^2} + \ldots + a{q^{n - 1}} \cr & q{s_n} = aq + a{q^2} + \ldots + a{q^{n - 1}} + a{q^n} \cr & {s_n} - q{s_n} = a - a{q^n} \cr & {s_n} = \frac{a}{{1 - q}} - \frac{{a{q^n}}}{{1 - q}} \cr} $$当$\left| q \right| < 1$时,由于$\mathop {\lim }\limits_{n \to \infty } {q^n} = 0$,从而$\mathop {{\text{lim}}}\limits_{n \to \infty } {s_n} = \frac{a}{{1 - q}}$,此时级数$\mathop \sum \limits_{n = 0}^\infty a{q^n}$收敛.
当$\left| q \right| > 1$时,由于$\mathop {\lim }\limits_{n \to \infty } {q^n} = \infty $,从而$\mathop {{\text{lim}}}\limits_{n \to \infty } {s_n} = \infty $,这时级数$\mathop \sum \limits_{n = 0}^\infty a{q^n}$发散.
如果$\left| q \right| = 1$,则当$q=1$时,$\mathop {{\text{lim}}}\limits_{n \to \infty } {s_n} = \mathop {{\text{lim}}}\limits_{n \to \infty } na = \infty $,因此级数发散;当$q=-1$时,
$$\mathop \sum \limits_{n = 0}^\infty a{q^n} = a - a + a - a + \ldots $$当$n$为偶数时(0是偶数),${s_n} = a$;当$n$为奇数时,${s_n} = 0$,因此,在$n \to \infty $时,${s_n}$在$a$与$0$之间跳跃,$\mathop {{\text{lim}}}\limits_{n \to \infty } {s_n}$的极限不存在,级数$\mathop \sum \limits_{n = 0}^\infty a{q^n}$发散.
我们可以将任意常数用几何级数展开,对任意常数$C$,取$q = \frac{1}{2}$,得
$$C = \frac{C}{2} + \frac{C}{4} + \ldots + \frac{C}{{{2^n}}} + \ldots $$早期的级数思想
级数的研究应用起源于西方,英语单词是series,将series翻译为级数,主要特征在于“级”字,即一列有等级、级差的数.最早出现的是公比小于1的几何级数.芝诺(约公元前490-前425, 意大利哲学家)有关运动的悖论之一,二分法,在亚里士多德写的《物理学》中被这样描述到:“移动是不可能的,因为在移动到终点位置之前,必须先移动到原位置与终点位置的中点处”.换句话说,为了走过一段直线,首先必须达到直线的中点,然后再到达直线的$\frac{1}{4}$处,然后是$\frac{1}{8}$,…,因此,移动永远没有开始.这个悖论蕴含着将1无限分割的思想,可以表示为公比为$\frac{1}{2}$的几何级数
$$1 = \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + ... + \frac{1}{{{2^{n}}}} + ...$$各种特殊面积、体积以及曲线段的求解促进了级数的发展.
古印度数学家(约公元前1000年)将圆切成许多小瓣,再把这些小瓣组合成一个长方形,用长方形的面积代替圆的面积;
古希腊(公元前800年-公元前146年)数学家从圆的内接正多边形和外切正多边形同时入手,不断增加它们的边数,从里外两个方面去逼近圆的面积;
开普勒(Johanns Ke-pler,1571-1630)认为,古代数学家用分割方法求圆面积时,分割次数有限,求出来的面积只是圆面积的近似值,开普勒把圆分割成无穷多个小扇形.因为扇形很小,弧$\widehat {AB}$也很短,所以$\widehat {AB} = \overline {AB} $,小扇形面积等于小三角形面积:$\frac{1}{2}R \cdot \overline {AB} $
圆面积$S$等于无穷多个小扇形的面积之和:
$$\eqalign{ & S = \frac{1}{2}R \cdot \overline {AB} + \frac{1}{2}R \cdot \overline {BC} + \ldots \cr & = \frac{1}{2}R \cdot (\overline {AB} + \overline {BC} + \ldots ) \cr & = \frac{1}{2}R \cdot 2\pi R \cr & = \pi {R^2} \cr} $$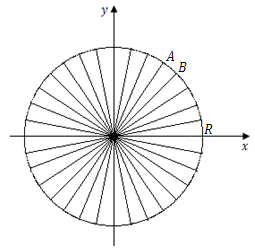
开普勒无法解答小扇形面积是否等于0的问题.如果等于0,那么小扇形面积就不存在,如果不等于0,那么小扇形面积与小三角形面积就不相等,将两者视为相等就是不对的.
卡瓦利里(Cavalier, Francesco Bonaventura 1598-1647)在开普勒研究的基础上,给出了“无穷小量”的概念:点是线的无穷小量,线是面的无穷小量,面是体积的无穷小量.
卡瓦利里通过“无穷小量”的概念和来自鲍格兰德(Jean Beau grand,1584-1640)的关于二项式系数的代数公式,得到了
$$\sum {{x^n}} = \frac{1}{{n + 1}}{a^{n + 1}}$$的重要结论,这个结论等价于
$$\int\limits_0^a {{x^n}{\text{d}}x} = \frac{{{a^{n + 1}}}}{{n + 1}}$$积分符号$\smallint $是字母s的拉长,是拉丁文summa(n.总数, 和)的第一个字母,最初由莱布尼茨使用.
如果$x$只取整数,则
$$\mathop {\lim }\limits_{a \to \infty } \frac{{{1^n} + {2^n} + \ldots + {a^n}}}{{{a^{n + 1}}}} = \frac{1}{{n + 1}}$$即
$$\mathop {\lim }\limits_{n \to \infty } \frac{{\sum {{i^k}} }}{{{n^{k + 1}}}} = \frac{1}{{k + 1}}$$卡瓦利里于1635年在他的书《几何学中不可分割的连续量》(Geometria indivisibilis continuorum)中首次发表了这一结果.
1668年,尼古拉斯•墨卡托发表了他的《对数技术》,在该书的第三部分,墨卡托通过计算双曲线$y = \frac{1}{{1 + x}}$下从0到$x$之间的面积,得到著名的墨卡托级数
$$\ln \left( {1 + x} \right) = x - \frac{{{x^2}}}{2} + \frac{{{x^3}}}{3} - \frac{{{x^4}}}{4} + \ldots $$墨卡托的推导过程不是很清楚,因此,我们给出沃利斯(Wallis)于同年在哲学学报上发表的《对数技术》的评论中,有关墨卡托级数的比较清晰的说明.
把区间$[0,x]$划分为n个相等小区间,每个小区间的长度$h = \frac{x}{n}$ ,构成n个小矩形,如下图所示,小矩形的高依次为
$$1,\frac{1}{{1 + h}},\frac{1}{{1 + 2h}}, \ldots ,\frac{1}{{1 + (n - 1)h}}$$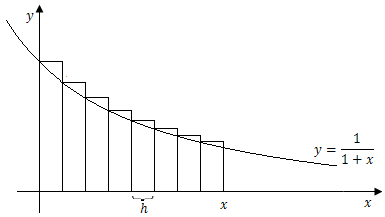
则所求面积
$$A \cong h + \frac{h}{{1 + h}} + \frac{h}{{1 + 2h}} + \ldots + \frac{h}{{1 + (n - 1)h}}$$现在将每个小矩形的高展开为几何级数,我们知道,对于几何级数
$$\mathop \sum \limits_{n = 0}^\infty a{q^n} = a + aq + a{q^2} + \ldots + a{q^n} + \ldots $$ $${s_n} = \frac{a}{{1 - q}} - \frac{{a{q^n}}}{{1 - q}}$$当$\left| q \right| < 1$时,由于$\mathop {\lim }\limits_{n \to \infty } {q^n} = 0$,从而$\mathop {{\text{lim}}}\limits_{n \to \infty } {s_n} = \frac{a}{{1 - q}}$
则
$$\eqalign{ & \frac{1}{{1 + h}} = \mathop \sum \limits_{n = 0}^\infty {( - 1)^n}{h^n} = 1 - h + {h^2} - {h^3} + \ldots \cr & \frac{1}{{1 + 2h}} = \mathop \sum \limits_{n = 0}^\infty {( - 1)^n}{(2h)^n} = 1 - 2h + {(2h)^2} - {(2h)^3} + \ldots \cr & \frac{1}{{1 + (n - 1)h}} = \mathop \sum \limits_{n = 0}^\infty {( - 1)^n}{[\left( {n - 1} \right)h]^n} \cr & = 1 - \left( {n - 1} \right)h + {[\left( {n - 1} \right)h]^2} - {[\left( {n - 1} \right)h]^3} + \ldots \cr} $$那么
$$\eqalign{ & A \cong h + \frac{h}{{1 + h}} + \frac{h}{{1 + 2h}} + \ldots + \frac{h}{{1 + (n - 1)h}} \cr & = h + h\left( {1 - h + {h^2} - {h^3} + \ldots } \right) \cr & + h\left( {1 - 2h + {{\left( {2h} \right)}^2} - {{\left( {2h} \right)}^3} + \ldots } \right) + \ldots \cr & + h(1 - \left( {n - 1} \right)h + {[\left( {n - 1} \right)h]^2} - {[\left( {n - 1} \right)h]^3} + \ldots ) \cr & = h + (h - {h^2} + {h^3} - {h^4} + ?) + [h - 2{h^2} + {(2)^2}{h^3} \cr & - {(2)^3}{h^4} + ...] + ... + [h - (n - 1){h^2} + {(n - 1)^2}{h^3} - {(n - 1)^3}{h^4} + ...] \cr & = nh - {h^2}\left[ {1 + 2 + 3 + \ldots + \left( {n - 1} \right)} \right] + {h^3}\left[ {1 + {2^2} + \ldots + {{\left( {n - 1} \right)}^2}} \right] \cr & . \cr & . \cr & . \cr & + {( - 1)^k}{h^{k + 1}}\left[ {{1^k} + {2^k} + \ldots + {{\left( {n - 1} \right)}^k}} \right] + \ldots \cr} $$(将$h = \frac{x}{n}$带入上式)
$$\eqalign{ & = x - \frac{{{x^2}}}{{{n^2}}}\left( {\mathop \sum \limits_{i = 1}^{n - 1} i} \right) + \frac{{{x^3}}}{{{n^3}}}\left( {\mathop \sum \limits_{i = 1}^{n - 1} {i^2}} \right) + \ldots + {\left( { - 1} \right)^k}\frac{{{x^{k + 1}}}}{{{n^{k + 1}}}}(\mathop \sum \limits_{i = 1}^{n - 1} {i^k}) \cr & = x - {x^2}\left( {\frac{1}{{{n^2}}}\mathop \sum \limits_{i = 1}^{n - 1} i} \right) + {x^3}\left( {\frac{1}{{{n^3}}}\mathop \sum \limits_{i = 1}^{n - 1} {i^2}} \right) + \ldots + {\left( { - 1} \right)^k}{x^{k + 1}}(\frac{1}{{{n^{k + 1}}}}\mathop \sum \limits_{i = 1}^{n - 1} {i^k}) \cr} $$现在,根据卡瓦利里得到的结论,
$$\mathop {\lim }\limits_{n \to \infty } \frac{{\sum {{i^k}} }}{{{n^{k + 1}}}} = \frac{1}{{k + 1}}$$得
$$A = x - \frac{{{x^2}}}{2} + \frac{{{x^3}}}{3} - \frac{{{x^4}}}{4} + \ldots $$而$A$是函数$y = \frac{1}{{1 + x}}$在0到$x$之间的积分,即
$$A = \int\limits_0^x {\frac{1}{{1 + x}}{\text{d}}x} = \ln \left( {1 + x} \right) = x - \frac{{{x^2}}}{2} + \frac{{{x^3}}}{3} - \frac{{{x^4}}}{4} + \ldots $$由此可知,对数函数$y = \ln \left( {1 + x} \right)$以级数展开,是对平面图形求面积的结果.
非线性函数分为代数函数和超越函数.超越函数是指函数不能用变量之间的有限次数的加、减、乘、除、乘方、开方运算表示的函数.比如对数函数,反三角函数,指数函数,三角函数等.
同济大学数学系编写的《高等数学》系列版教材中,对泰勒公式的讲解如下:
对于一些较复杂的函数,为了便于研究,往往希望用一些简单的函数来近似表达.由于多项式表示的函数,只要对自变量进行有限次数的加、减、乘三种算术运算,便能求出它的函数值来,因此我们经常用多项式来近似表达函数.
设函数$f\left( x \right)$在含有${x_0}$的开区间内具有直到$(n+1)$阶导数,试找出一个关于$\left( {x - {x_0}} \right)$的$n$次多项式
$${p_n}(x) = {a_0} + {a_1}\left( {x - {x_0}} \right) + {a_2}{\left( {x - {x_0}} \right)^2} + \ldots + {a_n}{\left( {x - {x_0}} \right)^n}$$来近似表达$f\left( x \right)$,要求${p_n}(x)$与$f\left( x \right)$之差是比${\left( {x - {x_0}} \right)^n}$高阶的无穷小,并给出误差$|f\left( x \right) - {p_n}(x)|$的具体表达式.
下面我们来讨论这个问题.假设${p_n}(x)$在${x_0}$处的函数值及它的直到$n$阶导数在${x_0}$处的值依次与$f({x_0}){\rm{,}}f'({x_0}){\rm{,}}...{\rm{,}}{f^{\left( n \right)}}({x_0})$相等,即满足
$${p_n}\left( {{x_0}} \right) = f\left( {{x_0}} \right),{p_n}'\left( {{x_0}} \right) = f'\left( {{x_0}} \right)$$ $$p_n^{''}\left( {{x_0}} \right) = {f^{''}}\left( {{x_0}} \right), \ldots ,p_n^{(n)}\left( {{x_0}} \right) = {f^{(n)}}\left( {{x_0}} \right)$$按这些等式来确定多项式${p_n}(x)$的系数${a_0},{a_1},{a_2}, \ldots ,{a_n}$,得
$${a_0} = f\left( {{x_0}} \right),{a_1} = f'\left( {{x_0}} \right),{a_2} = \frac{1}{{2!}}f''\left( {{x_0}} \right), \ldots ,{a_n} = \frac{1}{{n!}}{f^{(n)}}\left( {{x_0}} \right)$$得
$${p_n}(x) = $$ $$ f\left( {{x_0}} \right) + f'\left( {{x_0}} \right)\left( {x - {x_0}} \right) + \frac{{f''\left( {{x_0}} \right)}}{2}{\left( {x - {x_0}} \right)^2} + \ldots + \frac{{{f^{(n)}}\left( {{x_0}} \right)}}{{n!}}{\left( {x - {x_0}} \right)^n}$$泰勒(Taylor)中值定理 如果数$f\left( x \right)$在含有${x_0}$的某个开区间$(a,b)$内具有直到$n+1$阶的导数,则对任一$x \in (a,b)$,有
$$ \eqalign{ & f\left( x \right) = \cr & f\left( {x_0 } \right) + f'\left( {x_0 } \right)\left( {x - x_0 } \right) + {{f''\left( {x_0 } \right)} \over 2}\left( {x - x_0 } \right)^2 + ... + {{f^n \left( {x_0 } \right)} \over {n!}}\left( {x - x_0 } \right)^n \cr & + R_n \left( x \right) \cr} $$其中
$${R_n}\left( x \right) = \frac{{{f^{\left( {n + 1} \right)}}\left( \xi \right)}}{{\left( {n + 1} \right)!}}{(x - {x_0})^{n + 1}}$$这里$\xi $是${x_0}$与$x$之间的某个值.
证
对两个函数${R_n}\left( x \right)$及${(x - {x_0})^{n + 1}}$在以${x_0}$及$x$为端点的区间上应用柯西中值定理公式,得
$$\frac{{{R_n}\left( x \right)}}{{{{\left( {x - {x_0}} \right)}^{n + 1}}}} = \frac{{{R_n}\left( x \right) - {R_n}\left( {{x_0}} \right)}}{{{{\left( {x - {x_0}} \right)}^{n + 1}} - 0}} = \frac{{{R_n}'\left( {{\xi _1}} \right)}}{{(n + 1){{\left( {{\xi _1} - {x_0}} \right)}^n}}}$$(${\xi _1}$在$x$与$x_0$之间)
\begin{array}{l} = \frac{{{R_n}'\left( {{\xi _1}} \right) - {R_n}'\left( {{x_0}} \right)}}{{\left( {n + 1} \right){{\left( {{\xi _1} - {x_0}} \right)}^n} - 0}} = \frac{{{R_n}''({\xi _2})}}{{\left( {n + 1} \right){{\left( {{\xi _1} - {x_0}} \right)}^{n - 1}}}} = \ldots \\ = \frac{{R_n^{(n + 1)}(\xi )}}{{\left( {n + 1} \right)!}} \end{array}(${\xi}$在$x$与$x_0$之间)
一、问题
1.如何理解:多项式表示的函数,只要对自变量进行有限次数的加、减、乘三种算术运算,便能求出它的函数值来.
2.关于$\left( {x - {x_0}} \right)$的$n$次多项式
$${p_n}(x) = {a_0} + {a_1}\left( {x - {x_0}} \right) + {a_2}{\left( {x - {x_0}} \right)^2} + \ldots + {a_n}{\left( {x - {x_0}} \right)^n}$$是如何导出的.
3.证明过程中为何使用柯西(1789-1857)中值定理公式?
二、泰勒公式的推导
实际问题中的函数$f(x)$,有的表达式很复杂,有的甚至给不出表达式,只能通过某种测量方法得到一些离散的自变量-函数值对;一个很自然的想法就是,如何将$f(x)$用某个函数$P(x)$近似表示.
2.1 插值法求函数$f(x)$的近似表达式
2.1.1 插值函数P(x)的选择
2.1.2 线性插值
选择哪种函数类型$P(x)$来近似代替$f(x)$是我们首先需要考虑的问题,如果测得$f(x)$上的两个点${x_0},{x_1}$对应的函数值${y_0} = f\left( {{x_0}} \right),{y_1} = f({x_1})$,我们可以用线性函数${P_1}(x)$近似代替函数$f(x)$.
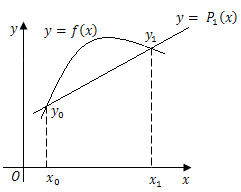
用点斜式表示
$${P_1}\left( x \right) = {y_0} + \frac{{{y_1} - {y_0}}}{{{x_1} - {x_0}}}\left( {x - {x_0}} \right)$$ $$ = f\left( {{x_0}} \right) + \frac{{f\left( {{x_1}} \right) - f\left( {{x_0}} \right)}}{{{x_1} - {x_0}}}\left( {x - {x_0}} \right)$$定义
$$f\left[ {{x_i},{x_j}} \right] = \frac{{f({x_j}) - f({x_i})}}{{{x_j} - {x_i}}}$$为f(x)在${x_i},{x_j}$处的一阶差商,则称
$${P_1}\left( x \right) = f\left( {{x_0}} \right) + f\left[ {{x_i},{x_j}} \right]\left( {x - {x_0}} \right)$$为一次牛顿线性插值函数.
用两点式表示
$${P_1}\left( x \right) = {y_0}\frac{{x - {x_1}}}{{{x_0} - {x_1}}} + {y_1}\frac{{x - {x_0}}}{{{x_1} - {x_0}}}$$记
$${l_0}\left( x \right) = \frac{{x - {x_1}}}{{{x_0} - {x_1}}},{l_1}\left( x \right) = \frac{{x - {x_0}}}{{{x_1} - {x_0}}}$$为一次插值基函数,则
$${P_1}\left( x \right) = {y_0}{l_0}\left( x \right) + {y_1}{l_1}\left( x \right)$$为一次拉格朗日线性插值函数.
如下表所示,$f(x)$在开区间$(a,b)$内具有直到$(n+1)$阶的导数,相异的点${x_i},i = 0,1,2, \ldots ,n$都在$[a,b]$上,不妨设$a \le {x_0} < {x_1} < {x_2} < \ldots < {x_n} \le b$,且$x$是$[a,b]$上一点,
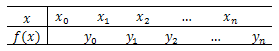
由于$f(x)$很复杂甚至数学表达式未知,我们希望构造另外一个函数$P(x)$,使得$P\left( {{x_{\rm{i}}}} \right) = {y_{\rm{i}}},i = 0,1,2,3, \ldots ,n$,用$P(x)$近似代替$f(x)$.为了便于叙述,通常称区间$[a,b]$为插值区间,点${x_0},{x_1}, \ldots {x_n}$为插值节点,函数$P(x)$为插值函数,求插值函数$P(x)$的方法称为插值法.
2.2 差商的定义及其性质
2.2.1差商的定义
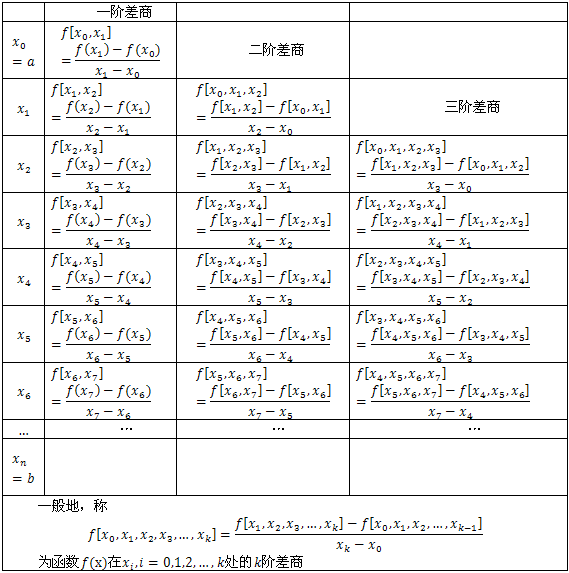
……
一般地,
$$f\left[ {{x_0},{x_1}, \ldots ,{x_k}} \right] = \mathop \sum \limits_{i = 0}^k \frac{{f({x_i})}}{{\left( {{x_i} - {x_0}} \right) \ldots \left( {{x_i} - {x_{i - 1}}} \right)\left( {{x_i} - {x_{i + 1}}} \right) \ldots \left( {{x_i} - {x_k}} \right)}}$$2.2.2 差商的性质
A. $f\left( x \right)$的$k$阶差商$f\left[ {{x_0},{x_1}, \ldots ,{x_k}} \right]$可由函数值$f\left( {{x_0}} \right),f\left( {{x_1}} \right), \ldots ,f({x_k})$的线性组合表示.
B. 差商与节点的顺序无关.
$$f\left[ {x,{x_0}} \right] = \frac{{f\left( x \right) - f({x_0})}}{{x - {x_0}}} \Rightarrow $$ $$f\left( x \right) = f\left( {{x_0}} \right) + f\left[ {x,{x_0}} \right](x - {x_0})$$ $$f\left[ {x,{x_0},{x_1}} \right] = \frac{{f\left[ {{x_0},{x_1}} \right] - f\left[ {x,{x_0}} \right]}}{{{x_1} - x}} \Rightarrow $$ $$f\left[ {x,{x_0}} \right] = f\left[ {{x_0},{x_1}} \right] + f\left[ {x,{x_0},{x_1}} \right](x - {x_1})$$ $$f\left( x \right) = f\left( {{x_0}} \right) + f\left[ {{x_0},{x_1}} \right]\left( {x - {x_0}} \right) + f\left[ {x,{x_0},{x_1}} \right](x - {x_0})(x - {x_1})$$ $$f\left[ {x,{x_0},{x_1},{x_2}} \right] = \frac{{f\left[ {{x_0},{x_1},{x_2}} \right] - f\left[ {x,{x_0},{x_1}} \right]}}{{{x_2} - x}} \Rightarrow $$ $$f\left[ {x,{x_0},{x_1}} \right] = f\left[ {{x_0},{x_1},{x_2}} \right] + f\left[ {x,{x_0},{x_1},{x_2}} \right](x - {x_2})$$ $$f\left( x \right) = f\left( {{x_0}} \right) + f\left[ {{x_0},{x_1}} \right]\left( {x - {x_0}} \right) + f\left[ {{x_0},{x_1},{x_2}} \right](x - {x_0})(x - {x_1})$$ $$ + f\left[ {x,{x_0},{x_1},{x_2}} \right](x - {x_0})(x - {x_1})(x - {x_2})$$……
$$ \begin{array}{l} f\left( x \right) = f\left( {{x_0}} \right) + f\left[ {{x_0},{x_1}} \right]\left( {x - {x_0}} \right) + f\left[ {{x_0},{x_1},{x_2}} \right]\left( {x - {x_0}} \right)\left( {x - {x_1}} \right)\\ + \ldots + f\left[ {x,{x_0},{x_1},{x_2}, \ldots ,{x_{n - 1}}} \right]\left( {x - {x_0}} \right)\left( {x - {x_1}} \right)\left( {x - {x_2}} \right) \ldots \left( {x - {x_{n - 1}}} \right)\\ f\left( x \right) = f\left( {{x_0}} \right) + f\left[ {{x_0},{x_1}} \right]\left( {x - {x_0}} \right) + f\left[ {{x_0},{x_1},{x_2}} \right]\left( {x - {x_0}} \right)\left( {x - {x_1}} \right) + \\ \ldots + f\left[ {x,{x_0},{x_1},{x_2}, \ldots ,{x_{n - 1}}} \right]\left( {x - {x_0}} \right)\left( {x - {x_1}} \right)\left( {x - {x_2}} \right) \ldots \left( {x - {x_{n - 1}}} \right) + \\ f\left[ {x,{x_0},{x_1},{x_2}, \ldots ,{x_{n - 1}},{x_n}} \right]\left( {x - {x_0}} \right)\left( {x - {x_1}} \right)\left( {x - {x_2}} \right) \ldots \left( {x - {x_{n - 1}}} \right)\left( {x - {x_n}} \right) \end{array} $$令
$$\begin{array}{l} {R_{\rm{n}}}\left( x \right) = \\ f\left[ {x,{x_0},{x_1},{x_2}, \ldots ,{x_{n - 1}},{x_n}} \right]\left( {x - {x_0}} \right)\left( {x - {x_1}} \right)\left( {x - {x_2}} \right) \ldots \left( {x - {x_{n - 1}}} \right)\left( {x - {x_n}} \right)\\ {P_{\rm{n}}}\left( x \right) = f\left( {{x_0}} \right) + f\left[ {{x_0},{x_1}} \right]\left( {x - {x_0}} \right) + f\left[ {{x_0},{x_1},{x_2}} \right]\left( {x - {x_0}} \right)\left( {x - {x_1}} \right)\\ + f\left[ {x,{x_0},{x_1},{x_2}} \right]\left( {x - {x_0}} \right)\left( {x - {x_1}} \right)\left( {x - {x_2}} \right) + \ldots \\ + f\left[ {x,{x_0},{x_1},{x_2}, \ldots ,{x_{n - 1}}} \right]\left( {x - {x_0}} \right)\left( {x - {x_1}} \right)\left( {x - {x_2}} \right) \ldots \left( {x - {x_{n - 1}}} \right) \end{array}$$则
$$\begin{array}{l} f\left( x \right) = {P_{\rm{n}}}\left( x \right) + {R_{\rm{n}}}(x)\\ {R_{\rm{n}}}(x) = f\left( x \right) - {P_{\rm{n}}}\left( x \right)\\ {R_{\rm{n}}}\left( {{x_0}} \right) = {R_{\rm{n}}}\left( {{x_1}} \right) = \ldots = {R_{\rm{n}}}\left( {{x_{\rm{n}}}} \right) = 0 \end{array}$$根据罗尔定理,有
$$\begin{array}{l} {R_{\rm{n}}}^{\left( {n + 1} \right)}\left( \xi \right) = {f^{\left( {n + 1} \right)}}\left( \xi \right) - {P_{\rm{n}}}^{\left( {n + 1} \right)}\left( \xi \right) = 0,(a < \xi < b)\\ {P_{\rm{n}}}^{\left( {n + 1} \right)}\left( \xi \right) = \left( {n + 1} \right)!f\left[ {x,{x_0},{x_1},{x_2}, \ldots ,{x_{n - 1}},{x_n}} \right] \end{array}$$得
$$f\left[ {x,{x_0},{x_1},{x_2}, \ldots ,{x_{n - 1}},{x_n}} \right] = \frac{{{f^{\left( {n + 1} \right)}}\left( \xi \right)}}{{\left( {n + 1} \right)!}},(a < \xi < b)$$所以
$$\begin{array}{l} f\left( x \right) = f\left( {{x_0}} \right) + f\left[ {x,{x_0}} \right]\left( {x - {x_0}} \right) + f\left[ {x,{x_0},{x_1}} \right]\left( {x - {x_0}} \right)\left( {x - {x_1}} \right) + \\ \ldots + f\left[ {x,{x_0},{x_1},{x_2}, \ldots ,{x_{n - 1}}} \right]\left( {x - {x_0}} \right)\left( {x - {x_1}} \right)\left( {x - {x_2}} \right) \ldots \left( {x - {x_{n - 1}}} \right) + \\ f\left[ {x,{x_0},{x_1},{x_2}, \ldots ,{x_{n - 1}},{x_n}} \right]\left( {x - {x_0}} \right)\left( {x - {x_1}} \right)\left( {x - {x_2}} \right) \ldots \left( {x - {x_{n - 1}}} \right)\left( {x - {x_n}} \right) \end{array}$$ $$\begin{array}{l} f\left( x \right) = f\left( {{x_0}} \right) + f'\left( {{\xi _0}} \right)\left( {x - {x_0}} \right) + \\ \frac{{f''\left( {{\xi _1}} \right)}}{2}\left( {x - {x_0}} \right)\left( {x - {x_1}} \right) + \ldots + \\ \frac{{{f^{(n)}}\left( {{\xi _n}} \right)}}{{n!}}\left( {x - {x_0}} \right)\left( {x - {x_1}} \right)\left( {x - {x_2}} \right) \ldots \left( {x - {x_{n - 1}}} \right) + {R_n}\left( x \right) \end{array}$$当$x \to {x_0}$时,${\xi _i},{x_i}$同时趋于${x_0}$,得
$$\begin{array}{l} f\left( x \right) = f\left( {{x_0}} \right) + f'\left( {{x_0}} \right)\left( {x - {x_0}} \right) + \frac{{f''\left( {{x_0}} \right)}}{2}{\left( {x - {x_0}} \right)^2} + \\ \ldots + \frac{{{f^{(n)}}\left( {{x_0}} \right)}}{{n!}}{\left( {x - {x_0}} \right)^n} + {R_n}\left( x \right) \end{array}$$其中
$${R_n}\left( x \right) = \frac{{{f^{\left( {n + 1} \right)}}\left( \xi \right)}}{{\left( {n + 1} \right)!}}{(x - {x_0})^{n + 1}}$$这里$\xi $是${x_0}$与$x$之间的某个值.
更容易理解的推导在教材下册级数部分.
