函数的极值及其求法

定义 设函数$f(x)$在点$x_0$的某邻域$U(x_0)$内有定义，如果对于去心邻域$\mathop U\limits^0 \left( {x_0 } \right)$内的任一$x$，有

$$f(x) < f(x_0 ) (或f(x) > f(x_0 ))$$

那么就称$f(x_0 )$是函数$f(x)$的一个极大值（或极小值）local (or relative) maximum&local minimum point.

使函数取得极大值或极小值的点称为函数的极值点.

下面再次给出第一章中函数在区间$I$上的最大值或最小值定义与之对比：

在区间$I$上有定义的函数$f(x)$，如果有$x_0∈I$，使得对于任一$x∈I$，都有

$$f(x) ≤ f(x_0 ) (f(x) ≥ f(x_0 ))$$

则称$f(x_0 )$是函数$f(x)$在区间$I$上的最大值（最小值） global (or absolute) minimum&global (or absolute) maximum.

分析两者的区别

极值的定义中是指点$x_0$是其去心邻域内的极大值（或极小值），是局部的（因为邻域通常比较小），而且邻域是开区间；最值定义中$x_0$是整个区间内的最大值（或最小值）.（不特指的情况下，可以是任何区间，不像极值定义里是限制为开区间）

在最值的定义中，有等号，即$f(x)≤f(x_0 )$(或$f(x)≥f(x_0 )$)，此时除了$x_0$点外的其它点也可能与$x_0$点的函数值相等，即便相等，我们依然知道这个相等的值就是最大或最小值，不妨碍我们确认这个值.

从英文上来看，极值是local (or relative) - 小范围内相对而言我是最大或最小的，没有其它点了；最值是global (or absolute) - 全局的，绝对的（最大最小的值显然只有一个，是absolute的）.

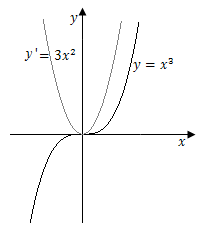
由费马原理可知，如果函数$f(x)$在$x_0$处可导，且$f(x)$在$x_0$处取得极值，那么$f'(x_0 )=0$，也就是说极值点一定是驻点，但是驻点不一定是函数的极值点，比如函数$y=x^3 (y'=3x^2)$在点$x=0$处是驻点，但不是极值点.

因此，驻点是可导函数取得极值的必要条件.

此外，函数在它的导数不存在的点处也可能取得极值，例如函数$f(x)=|x|$在点$x=0$处不可导，但函数在该点取得极小值.

定理2（第一充分条件）设函数$f(x)$在$x_0$连续，且在$x_0$的某去心邻域$\mathop U\limits^0 \left( {x_0 } \right)$内可导.

(1)若$x∈(x_0-δ,x_0)$ 时，$f'(x)>0$，而$x∈(x_0,x_0+δ)$ 时，$f'(x)<0$，则$f(x)$在$x_0$处取得极大值.

(2)若$x∈(x_0-δ,x_0)$ 时，$f'(x)<0$，而$x∈(x_0,x_0+δ)$ 时，$f'(x)>0$，则$f(x)$在$x_0$处取得极小值.

(3)若$x∈\mathop U\limits^0 \left( {x_0,δ } \right)$ 时，$f'(x)$的符号保持不变，则$f(x)$在$x_0$处没有极值.

证明：就情形（1）来说，当$x∈(x_0-δ,x_0) $时，$f'(x)>0$，设$x_1$是$(x_0-δ,x_0)$内任一点，则

$$\mathop {\lim }\limits_{x \to {x_1}} \frac{{f\left( x \right) - f({x_1})}}{{x - {x_1}}} = f'\left( {{x_1}} \right) > 0$$

根据函数极限的保号性，在$x∈\mathop U\limits^0 \left( {x_1 } \right) \subseteq ({x_0} - {\delta},{x_0})$内，有

$$\frac{{f\left( x \right) - f({x_1})}}{{x - {x_1}}} > 0$$

根据函数单调性的判断法，函数$f(x)$在$(x_0-δ,x_0)$内单调增加，

则当$x > x_1$时，$f(x)-f(x_1 )>0$，由于函数$f(x)$在$x_0$处是连续的，则

$$\mathop {\lim }\limits_{x \to {x_0}} [f\left( x \right) - f\left( {{x_1}} \right)] = f\left( {{x_0}} \right) - f\left( {{x_1}} \right)$$

根据函数极限的保号性，有

$$\mathop {\lim }\limits_{x \to {x_0}} [f\left( x \right) - f\left( {{x_1}} \right)] = f\left( {{x_0}} \right) - f\left( {{x_1}} \right) > 0$$

即$f(x_0 ) > f(x_1 )$

当$x < x_1$时，$f(x)-f(x_1 ) <0 $，由于函数$f(x)$在$x_0$处是连续的，则

$$\mathop {\lim }\limits_{{x_1} \to {x_0}} f\left( x \right) - f\left( {{x_1}} \right) = f\left( x \right) - f\left( {{x_0}} \right)$$

根据函数极限的保号性，有

$$\mathop {\lim }\limits_{{x_1} \to {x_0}} f\left( x \right) - f\left( {{x_1}} \right) = f\left( x \right) - f\left( {{x_0}} \right) < 0$$

即$f(x) < f(x_0 )$

因此当$x∈(x_0-δ,x_0)$ 时，$f(x) < f(x_0 )$

同理，当$x∈(x_0,x_0+δ)$ 时，$f(x) < f(x_0 )$

那么在$x∈\mathop U\limits^0 \left( {x_0} \right)$时，总有$f(x) < f(x_0 )$ ，所以$f(x_0 )$是$f(x)$的一个极大值.

类似的可以证明其他的情形.

 

定理3（第二充分条件）设函数$f(x)$在$x_0$处具有二阶导数且$f'(x_0 )=0 $，$f''(x_0 )≠0$，那么

(1)当$f''(x_0 )<0 $时，函数$f(x)$在$x_0$处取得极大值；

(2)当$f''(x_0 )>0$ 时，函数$f(x)$在$x_0$处取得极小值；

证明:在情形（1），由于$f''(x_0 )<0$按照二阶导数的定义有，

$$f''\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f'\left( x \right) - f'({x_0})}}{{x - {x_0}}} < 0$$

但$f'(x_0 )=0$，所以上式即

$$\frac{{f'\left( x \right)}}{{x - {x_0}}} < 0$$

因此，当$x < x_0$时，$f'(x)>0$；当$x>x_0$时，$f'(x)<0$，根据定理2可知，$f(x)$在点$x_0$处取得极大值.

类似的可以证明情形（2）.

当$f''(x_0 )=0$时，$f(x)$在$x_0$处可能取得极大值，也可能取得极小值，也可能没有极值，例如$f_1=-x^4$，$f_2=x^4$，$f_3=x^3$这三个函数在$x=0$处分别取得极大值，极小值和没有极值，因此，如果函数在驻点处的二阶导数为零，那么还得用一阶导数在驻点左右邻近的符号来判断.