曲线的凹凸性与拐点

函数的单调性反映在图形上，就是曲线的上升或下降，但是在上升或下降的过程中还有一个弯曲方向的问题，也就是曲线的凹凸性.

如果曲线弧总是位于连结曲线上任意两点间的弦的上方，则称曲线是向上凸的；如果曲线弧总是位于连结曲线上任意两点间的弦的下方，则称曲线是向上凹的，曲线的这种性质就是曲线的凹凸性.因此，曲线的凹凸性可以用连结曲线弧上任意两点的弦的中点与曲线弧上相应点（即具有相同横坐标的点）的位置关系来描述.

定义 设$f(x)$在区间$I$上连续，如果对于$I$上的任意两点$x_1$,$x_2$恒有

$$f\left( {\frac{{{x_1} + {x_2}}}{2}} \right) < \frac{{f\left( {{x_1}} \right) + f({x_2})}}{2}$$

那么称$f(x)$在$I$上图像是（向上）凹的（或凹弧）；如果恒有

$$f\left( {\frac{{{x_1} + {x_2}}}{2}} \right) > \frac{{f\left( {{x_1}} \right) + f({x_2})}}{2}$$

那么称$f(x)$在$I$上图像是（向上）凸的（或凸弧）

定理2 设$f(x)$在$[a,b]$上连续，在$(a,b) $内具有一阶和二阶导数，那么

(1)若在$(a,b)$内$f''\left( x \right) > 0$，则$f(x)$在$[a,b]$上的图形是向上凹的；

(2)若在$(a,b)$内$f''\left( x \right) < 0$，则$f(x)$在$[a,b]$上的图形是向上凸的.

从运动学方程的位移、速度和加速度容易理解此定理，或者在曲线上画出切线，从切线的斜率(一阶导数)的变化（二阶导数）可以看出曲线的凹凸性，比如切线斜率变大，则是凹的.下面应用拉格朗日中值定理证明.

证明 （1）:设$x_1$和$x_2$为$[a,b]$内任意两点，且$x_1 < x_2$ ，记$\frac{{{x_1} + {x_2}}}{2} = {x_0}$,并记$x_2-x_0=x_0-x_1=h$，则$x_1=x_0-h$，$x_2=x_0+h$，由拉格朗日中值定理的公式可得

$$13. f(x_0+h)-f(x_0 )=f' (x_0+θ_1 h)h$$ $$12. f(x_0 )-f(x_0-h)=f' (x_0-θ_2 h)h$$

11. 其中$0 < θ_1 < 1,0 < θ_2 < 1$

10. 两式相减得

$$9. f(x_0+h)+f(x_0-h)-2f(x_0 )=[f' (x_0+θ_1 h)-f' (x_0-θ_2 h)]h$$

8. 对$f' (x)$在区间$[x_0-θ_2 h,x_0+θ_1 h]$上再次应用拉格朗日中值定理公式，得

$$7. f' (x_0+θ_1 h)-f' (x_0-θ_2 h)=f'' (ξ)(θ_1+θ_2)h$$ $$7'. [f' (x_0+θ_1 h)-f' (x_0-θ_2 h)]h=f'' (ξ)(θ_1+θ_2)h^2$$

6. 其中$x_0-θ_2 h < ξ < x_0+θ_1 h$

5. 若$f'' (ξ)>0$，则

$$4. f(x_0+h)+f(x_0-h)-2f(x_0 ) > 0$$ $$3. f(x_0+h)+f(x_0-h) > 2f(x_0 )$$ $$2.\frac{{f\left( {{x_0} + h} \right) + f\left( {{x_0} - h} \right)}}{2} > f\left( {{x_0}} \right)$$ $$1.\frac{{f\left( {{x_2}} \right) + f\left( {{x_1}} \right)}}{2} > f\left( {\frac{{{x_1} + {x_2}}}{2}} \right)$$

所以$f(x)$在$[a,b]$上的图形是向上凹的，类似的可以证明（2）.

 

一般地，如果$x_0$是在区间$I$上连续的函数$y=f(x)$的内点(区间$I$端点外的点)，如果曲线$y=f(x)$在经过点$(x_0,f(x_0)) $时，曲线的凹凸性改变了，那么就称点$(x_0,f(x_0))$为曲线的拐点.

导数为0的点称为函数的临界点或驻点.

我们可以按照以下步骤来判定区间$I$上的连续曲线$y=f(x)$的拐点：

(1)求$f'' (x)=0$的点

(2)求出区间$I$上$f'' (x)$不存在的点，并判断该点左右两侧邻近的符号，如果符号相反时，该点是拐点；符号相同时不是拐点.

 

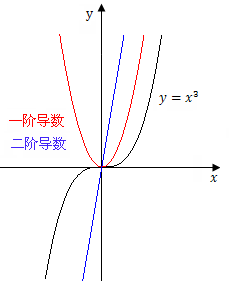
例 判断曲线$y=x^3$的凹凸性.

解$y'=3x^2，y''=6x$

当$x<0$时，$y''<0$，曲线在$(-∞,0]$上式向上凸的

当$x>0$时，$y''>0$，曲线在$[0,+∞)$上式向上凹的.

 

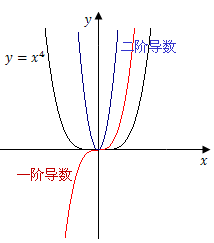
例 判断曲线$y=x^4$的凹凸性.

解 $y'=4x^3，y''=12x^2$

当$x≠0$时，$y''>0，x=0$时，$y''=0$，所以

曲线在$(-∞,-∞)$上式向上凹的.

 

例 求曲线$y = \root 3 \of x $的拐点.

解 函数在$(-∞,+∞)$上连续，

$$y' = \frac{1}{{3\root 3 \of {{x^2}} }},y'' = \frac{1}{{9x\root 3 \of {{x^2}} }}$$

$x=0$时$y',y''$都没有定义，通过判断判断$x=0$两侧$y''$的正负号，可知点$(0,0)$是拐点.