拉格朗日中值定理

如果函数$f(x)$满足

(1) 在闭区间$[a,b]$上连续；

(2) 在开区间$(a,b)$内可导；

那么在$(a,b)$内至少有一点$\xi (a < \xi < b)$，使等式$f(b)-f(a)=f' (ξ)(b-a)$成立.

证明：将$f(b)-f(a)=f' (ξ)(b-a)$写成：

$$\frac{{f\left( b \right) - f\left( a \right)}}{{b - a}} = f'\left( \xi \right)$$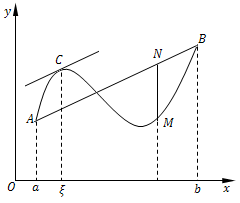

由图可见，$\frac{{f\left( b \right) - f\left( a \right)}}{{b - a}}$是弦$AB$的斜率，$f' (ξ)$是曲线在点$C$处的切线的斜率.因此拉格朗日中值定理的几何意义是：如果连续曲线$y=f(x)$的弧$\widehat {AB}$上除端点外处处具有不垂直于$x$轴的切线（即在开区间$(a,b)$内可导），那么这弧上至少有一点$C$，使曲线在$C$点处的切线平行于弦$AB$.

此定理和罗尔定理的区别在于$f(b)≠f(a)$，可见罗尔定理是拉格朗日中值定理的特殊情形.

我们希望利用罗尔定理来证明拉格朗日中值定理，因此需要构造一个在闭区间$[a,b]$上连续、在开区间$(a,b)$内可导的函数，使得该函数在点$a,b$处的函数值相等.

由图可见，有向线段$NM$的值（因为$NM$平行于$y$轴，因此$NM$的值等于终点纵坐标减起点纵坐标，值为正时，方向与$y$轴正方向一致；值为负时，方向与$y$轴正方向相反.）是$x$的函数，把它表示为$φ(x)$，且$φ(a)=φ(b)=0$，为了求出$φ(x)$的表达式，设直线$AB$的方程为$y=L(x)$，则

$$L\left( x \right) = f\left( a \right) + \frac{{f\left( b \right) - f\left( a \right)}}{{b - a}}(x - a)$$

由于点$N、M$的纵坐标依次为$L(x)$和$f(x)$，因此表示有向线段$NM$的值的函数

$$\varphi \left( x \right) = f\left( x \right) - L\left( x \right) = f\left( x \right) - f(a) - \frac{{f\left( b \right) - f\left( a \right)}}{{b - a}}(x - a)$$

由表达式可知：1.$φ(x)$是在闭区间$[a,b]$上连续的函数的和，根据连续函数的和、差、积、商的连续性定理，$φ(x)$在闭区间$[a,b]$上连续；2. $φ(x)$在开区间$(a,b)$内可导，且在区间端点处的函数值相等，根据罗尔定理，可知在$(a,b)$内至少有一点$ξ$，使$φ'(ξ)=0$，即

$$\eqalign{ & f'\left( \xi \right) - \frac{{f\left( b \right) - f\left( a \right)}}{{b - a}} = 0 \cr & f'\left( \xi \right) = \frac{{f\left( b \right) - f\left( a \right)}}{{b - a}} \cr} $$

即

$$f\left( b \right) - f\left( a \right) = f'\left( \xi \right)(b - a)$$

设x为区间[a,b]内一点，$x + \Delta x$为这一区间内的另一点（$\Delta x > 0$或$\Delta x < 0$），则在区间$[x,x + \Delta x]$，(当$\Delta x > 0$)或在区间$[x + \Delta x,x]$，(当$\Delta x < 0$)上就有

$$f\left( {x + \Delta x} \right) - f\left( x \right) = f'\left( {x + \theta \Delta x} \right)\Delta x,(0 < \theta < 1)$$

将$f(x)$记为$y$，则

$$\Delta y = f'\left( {x + \theta \Delta x} \right)\Delta x,(0 < \theta < 1)$$

拉格朗日中值定理的“中值”是指在开区间$(a,b)$内至少存在一点$ξ$，有上面的等式存在，主要强调的是在$a,b$的中间有值$ξ$满足$f(b)-f(a)=f' (ξ)(b-a).$

虽然$\Delta y = f'\left( {x + \theta \Delta x} \right)\Delta x,(0 < \theta < 1)$是精确值，但是$θ$不确定，函数的微分${\text{d}}y = f'(x) \cdot \Delta x$也只是$\Delta y$的近似计算式.

定理 如果函数$f(x)$在区间$I$上的导数恒为零，那么$f(x)$在区间$I$上是一个常数.

证明：在区间$I$上任意取两点$x_1$,$x_2$ ($x_1 < x_2$)，应用拉格朗日中值定理得

$$f\left( {{x_2}} \right) - f\left( {{x_1}} \right) = f'\left( \xi \right)\left( {{x_2} - {x_1}} \right)({x_1} < \xi < {x_2})$$

由假定，$f' (ξ)=0$，所以$f(x_2 )-f(x_1 )=0$，即

$$f(x_2 )=f(x_1 )$$

因为$x_1，x_2$是任意选的，因此$f(x)$在区间$I$上的函数值总是相等，也就是，$f(x)$在区间$I$上是一个常数.

例 证明当$x>0$时，

$$\frac{x}{{1 + x}} < \ln (1 + x) < x$$

证明：设$f\left( x \right) = \ln \left( {1 + x} \right)$，$f(x)$是初等函数，初等函数在定义区间连续，并且在定义区间内可导，所以在区间$[0,x]$上应用拉格朗日中值定理得：

$$f\left( x \right) - f\left( 0 \right) = f'\left( \xi \right)\left( {x - 0} \right)(0 < \xi < x)$$ $$f\left( 0 \right) = 0,f\left( x \right) = f'\left( \xi \right) \cdot x$$

即

$$\ln (1 + x) = \frac{x}{{1 + \xi }}$$

由于$0 < ξ < x$，所以

$$\frac{x}{{1 + x}} < \ln (1 + x) < x.$$