第三章 微分中值定理

这一章将应用函数的导数来研究函数以及曲线，并用这些知识解决一些实际问题. 首先介绍几个导数应用的理论基础：微分学的几个中值定理.

罗尔定理

费马引理 设函数$f(x)$在点$x_0$的某个邻域$U(x_0)$ 内有定义，并且在$x_0$处可导，如果对任意的$x∈U(x_0)$，有 $$f(x)≤f(x_0 ) (或f(x)≥f(x_0))$$ 那么$f'(x_0 )=0.$

证明：目的是证明$f'(x_0 )=0.$

我们用定义来证明，对于任意的$x∈U(x_0 )$，

$f(x)≤f(x_0 ) $时，$f(x)-f(x_0 )≤0$，分两种情况讨论，

$(1)f(x)=c(c是常数)$，那么$f(x)=f(x_0 )=c$，所以$f'(x_0 )=0.$

$(2)f(x)$不是常数，只有当$x=x_0$时，$f(x)=f(x_0 )，$

当$\Delta x = x - {x_0} > 0$时，

$$\frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}} < 0$$

当$\Delta x = x - {x_0} < 0$时,

$$\frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}} > 0$$

但是由于$f(x)$在$x_0$处可导，有 $$f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{\Delta x \to {0 }} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{\Delta x}} $$ 根据极限保号性的推论，无论导数$f'(x_0)$大于0或小于0都只能满足上述1种情况，因此导数既不大于0也不小于0.

保号性的推论：函数$f(x)$在$x∈U(x_0)$内，有$\frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}} \leqslant 0$，则$\mathop {\lim }\limits_{\Delta x \to 0} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{\Delta x}} = A \leqslant 0$.

$(3) f(x)$不是常数，当$x∈U(x_0)$时，也有$f({x_n}) = f({x_0})$，也就是说，不仅仅是$x=x_0$时，$f(x)=f(x_0 )$，则

当$\Delta x = x - {x_0} > 0$时，

$$\frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}} \leqslant 0$$

当$\Delta x = x - {x_0} < 0$时,

$$\frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}} \geqslant 0$$

函数$f(x)$在点$x_0$可导及极限的保号性的推论可得

$$f'\left( {{x_0}} \right) = f{'_ + }\left( {{x_0}} \right) = \mathop {\lim }\limits_{\Delta x \to {0^ + }} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{\Delta x}} \leqslant 0$$ $$f'\left( {{x_0}} \right) = f{'_ - }\left( {{x_0}} \right) = \mathop {\lim }\limits_{\Delta x \to {0^ - }} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{\Delta x}} \geqslant 0$$

所以$f'(x_0 )=0$.

 

推论 如果在$x_0$的某去心邻域内$f(x) \geqslant 0$（或$f(x) \leqslant 0$ ），而且$\mathop {\lim }\limits_{x \to {x_0}} f(x) = A$，那么$A \geqslant 0$(或$A \leqslant 0$).

对于任意的$x∈U(x_0 )，f(x)≥f(x_0 ) $时，有同样的证明.

费马引理的意思是：如果函数$f(x)$在$x∈U(x_0 )$内有定义，在$x_0$处可导，并且在$x∈U(x_0 )$上，$f(x_0 )$是最大值或最小值，那么函数$f(x)$在点$x_0$处的导数等于0.

通常称导数等于零的点为函数的驻点（或稳定点，临界点）.

我们举例来验证费马引理中$f(x)$不是常数的情况.

函数$y = \cos x$在$x_0=0$的某个邻域$U(x_0)$内有定义，并且在$x_0=0$处可导，对于任意的$x∈U(x_0)$，有$f(x)≤f(x_0)$，即$\cos ({x_0} + \Delta x) - \cos {x_0} \leqslant 0$

当$\Delta x = x - {x_0} > 0$时

$$\frac{{\cos ({x_0} + \Delta x) - \cos {x_0}}}{{\Delta x}} < 0$$

当$\Delta x = x - {x_0} < 0$时

$$\frac{{\cos ({x_0} + \Delta x) - \cos {x_0}}}{{\Delta x}} > 0$$ $$\eqalign{ & f'\left( {{x_0}} \right) = f{'_ + }\left( {{x_0}} \right) = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{\Delta x}} \cr & = \mathop {{\text{lim}}}\limits_{\Delta x \to {0^ + }} \frac{{\cos \left( {{x_0} + \Delta x} \right) - \cos {x_0}}}{{\Delta x}} \cr & = \mathop {{\text{lim}}}\limits_{\Delta x \to {0^ + }} \left[ {\frac{{ - 2\sin \left( {{x_0} + \frac{{\Delta x}}{2}} \right)\sin \frac{{\Delta x}}{2}}}{{\Delta x}}} \right] \cr & = \mathop {{\text{lim}}}\limits_{\Delta x \to {0^ + }} \left[ { - \sin \left( {{x_0} + \frac{{\Delta x}}{2}} \right) \cdot \frac{{\sin \frac{{\Delta x}}{2}}}{{\frac{{\Delta x}}{2}}}} \right] \cr & = \mathop {{\text{lim}}}\limits_{\Delta x \to {0^ + }} \left[ { - \sin \left( {{x_0} + \frac{{\Delta x}}{2}} \right)} \right] \cr & = - \sin {x_0} = 0. \cr} $$

 

$$\eqalign{ & f'\left( {{x_0}} \right) = f{'_ - }\left( {{x_0}} \right) = \mathop {\lim }\limits_{\Delta x \to {0^ - }} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{\Delta x}} \cr & = \mathop {{\text{lim}}}\limits_{\Delta x \to {0^ - }} \frac{{\cos \left( {{x_0} + \Delta x} \right) - \cos {x_0}}}{{\Delta x}} \cr & = \mathop {{\text{lim}}}\limits_{\Delta x \to {0^ - }} \left[ {\frac{{ - 2\sin \left( {{x_0} + \frac{{\Delta x}}{2}} \right)\sin \frac{{\Delta x}}{2}}}{{\Delta x}}} \right] \cr & = \mathop {{\text{lim}}}\limits_{\Delta x \to {0^ - }} \left[ { - \sin \left( {{x_0} + \frac{{\Delta x}}{2}} \right) \cdot \frac{{\sin \frac{{\Delta x}}{2}}}{{\frac{{\Delta x}}{2}}}} \right] \cr & = \mathop {{\text{lim}}}\limits_{\Delta x \to {0^ - }} \left[ { - \sin \left( {{x_0} + \frac{{\Delta x}}{2}} \right)} \right] \cr & = - \sin {x_0} = 0. \cr} $$

所以$f'\left( {{x_0}} \right) = \cos {'}0 = 0.$

上面的例子中，只有$x_0=0$时$f(x)=f(x_0)$.

“如果对任意的$x∈U(x_0)，$有$f(x)≤f(x_0 )$ (或$f(x)≥f(x_0))$”

的正确意思是，$f(x)$包含了$f(x)=c$和$f(x)$只在$x=x_0$处有$f(x)=f(x_0 )$或$x$在$U(x_0)$的除了$x_0$以外的其他点也有$f(x)=f(x_0 )$.

注意区分最大值、最小值与最大值点最小值点.

 

罗尔定理 如果函数$f(x)$满足

（1）在闭区间$[a,b]$上连续；

（2）在开区间$(a,b)$内可导；

（3）在区间端点处的函数值相等，即$f(a)=f(b)$ ，

那么在$(a,b)$内至少存在一点$\xi (a < \xi < b)$，使得$f'(ξ)=0.$

证明：函数$f(x)$在闭区间$[a,b]$上连续，根据闭区间上连续函数的性质，函数$f(x)$在闭区间$[a,b]$上必存在最大值$M$和最小值$m$，

$M=m$，则$f(x)=M$，$\forall x \in \left( {a,b} \right),f'\left( x \right) = 0.$

若$M>m$，因为$f(a)=f(b)$，所以$M$和$m$这两个数中至少有一个不等于$f(x)$在区间$[a,b]$端点处的函数值.不防设$M≠f(a)=f(b)$，那么在$(a,b)$内至少存在一点$ξ$使$f(ξ)=M$. 因此，$\forall x \in [a,b]$,有$f(x)≤f(ξ)$，由费马引理可得$f'(ξ)=0.$

我们使用了“$\forall x \in [a,b]$,有$f(x)≤f(ξ)$”，是闭区间，而费马引理是开区间，但是由于$M≠f(a)=f(b)$，所以这里实际考虑的是开区间$(a,b)$，所以用费马引理，符合引理中开区间的条件，所以实际上“$\forall x \in [a,b]$要改为“$\forall x \in (a,b)$.

我们可以将条件（2）修改为在闭区间$[a,b]$内可导，此时的可导性包括了单侧可导，是可导的特例，由于定理的普适性（定理之所以称为定理，就在于其普适性，即放之四海而皆准，不是仅用于特例.）而使用开区间$(a,b)$.无论条件（2）是开区间或闭区间，通过证明过程可知，都可以在不包括端点的开区间$(a,b)$内至少有一点$ξ$.

（1）在闭区间$[a,b]$上连续；（需要用到闭区间上连续的函数存在极大值和极小值的性质，从而运用费马引理）.

（2）在开区间$(a,b)$内可导；（分析：$\left( {a,b} \right) = \{ x|a < x < b\} $，不包括端点$a$和$b$，单侧可导是可导的特例，此处作为定理需要具有普遍性，应此使用在开区间$(a,b)$内可导.（2）的目的是将区间端点去掉.

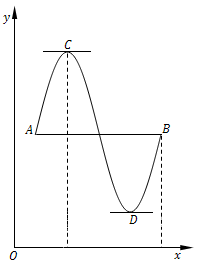
图中的曲线弧$\widehat {AB}$是函数$y=f(x)(x∈[a,b])$的图形.这是一条连续的曲线弧，除端点外处处有不垂直于$x$轴的切线，且两个端点的纵坐标相等，即$f(a)=f(b)$. 可以发现曲线弧的最高点$C$处或最低点$D$处，曲线有水平的切线，如果记$C$点的横坐标为$ξ$，则$f(ξ)=0$，这就是罗尔定理的几何描述.