第二章 函数的导数与微分

函数的极限和连续性概念是自洽的，也就是说两者可以相互推导，成为一个系统.如果说极限理论是基于某些具体实际得到的，是对这些实际的描述，那么连续性就是在此基础上的理论升华，使极限理论借助连续性概念成为一种通用理论并应用于广泛的问题中，然后再次反馈回来检验极限理论的正确性.

函数的极限和连续性概念是微积分学的基础，导数概念就是在此基础上建立起来的.位移函数$s=f(t)$的导数$v=f'(t)$精确地等于$t$时刻物体的瞬时速度，理解这一点也需要函数的极限和连续性概念.

引例

我们通过两个例子来引出导数的概念.

引例1不变向直线运动的速度

设某点沿直线向同一个方向运动.在直线上规定原点、正方向和单位长度，使直线成为数轴.再取定一个时刻作为测量时间的零点.则动点的位置坐标$s$与时间$t$之间具有某种函数关系：

$$s = f(t)$$

设从时刻$t_0$到$t$的时间间隔$t-t_0$内，动点从位置$s_0=f(t_0)$移动到$s=f(t)$，则动点在这段时间内运动的平均速度为

$$v = \frac{{s - {s_0}}}{{t - {t_0}}} = \frac{{f(t) - f({t_0})}}{{t - {t_0}}}$$

如果在动点的运动过程中任意选取$t_0$和$t$时，$v$都相同，那么动点的运动称为匀速直线运动，此时动点在任意一时刻的瞬时速度都与$v$相同；如果在动点的运动过程中任意选取$t_0$和$t$时，$v$不都是相同的，则动点作不变向变速直线运动，动点在每一时刻的瞬时速度都不尽相同；如何求该动点在某一时刻的瞬时速度呢？我们将时间间隔选取得较短，则上述比值在实践中也可以用来说明动点在时刻$t_0$的瞬时速度. 但是对于动点在$t_0$时刻的速度的精确概念来说，应当是：令$t→t_0$，求上述比值的极限.

用“令$t→t_0$，求上述比值的极限”定义动点在运动过程中任意时刻的瞬时速度是合理的.首先，瞬时速度也是速度，既然是速度，就必然满足速度的定义式

$$v = \frac{{\Delta s}}{{\Delta t}}$$

这要求时间间隔${\Delta t}$不等于0；其次，对于瞬时速度而言，我们需要的是某一时刻的速度，如果单纯考虑某一时刻，则时间变化量${\Delta t}$=0，这与速度的定义式矛盾，因此我们要令$t→t_0$，即$t$无限接近$t_0$又不等$t_0$时的比值的极限来表示某一时刻的瞬时速度.即

$$v = \mathop {\lim }\limits_{t \to {t_0}} \frac{{f\left( t \right) - f({t_0})}}{{t - {t_0}}}$$

注意，以后利用上面的公式求极限时，对于具体的某个函数$f(t)$，$\frac{{f(t) - f({t_0})}}{{t - {t_0}}}$将会化简为一个连续函数，比如$f(t)=2t^2+5$，有

$$v = \mathop {\lim }\limits_{t \to {t_0}} \frac{{f(t) - f({t_0})}}{{t - {t_0}}} = \mathop {\lim }\limits_{t \to {t_0}} \frac{{2{t^2} + 5 - 2t_0^2 - 5}}{{t - {t_0}}} = \mathop {\lim }\limits_{t \to {t_0}} \frac{{2(t + {t_0})(t - {t_0})}}{{t - {t_0}}}$$

最终，求$\frac{{2{t^2} + 5 - 2t_0^2 - 5}}{{t - {t_0}}}$的极限转化为求$\frac{{2(t + {t_0})(t - {t_0})}}{{t - {t_0}}}$的极限，显然，函数$\frac{{2(t + {t_0})(t - {t_0})}}{{t - {t_0}}}$的分母不能为零，于是约去公因子$t-t_0$，化简为求$2(t+t_0)$的极限了，此时，从不能取$t=t_0$，转化为可以取$t=t_0$，

$$\mathop {\lim }\limits_{t \to {t_0}} 2(t + {t_0}) = 4{t_0},$$

这个极限值$4t_0$是使$t=t_0$时得到的，如果它表示速度，则是$t=t_0$时的速度，而不是$t$无限趋于但不等于$t_0$（比如$t=0.9999t_0$）时的速度，所以我们最终求出来的速度，就是$t=t_0$时刻的瞬时速度，数值上精确地等于$t_0$时刻的瞬时速度.

导数精确表示瞬时速度的思考过程：

1.速度的定义式$v = \frac{{\Delta s}}{{\Delta t}}$决定了$\Delta t$不能取0，而瞬时速度要求$\Delta t$必须为0，我们用极限$v = \mathop {\lim }\limits_{t \to {t_0}} \frac{{f(t) - f({t_0})}}{{t - {t_0}}}$表示瞬时速度，其中的极限思想（$t→t_0$）表达了$\Delta t$不等于0；

2.极限值$v$存在，那么$v$就是该时刻（ $\Delta t = 0$）时的瞬时速度，这里应用到函数的连续性.连续性和极限之间的关系，是思考第2点的基础.

引例2切线问题

曲线上某点处的切线，是用无穷小的比较给出的概念（瞬时速度也是）.

设有曲线$C$及$C$上的一点$M$，在$C$上另取一点$N$，作割线$MN$.割线的斜率为

$$\tan \alpha = \frac{{y - {y_0}}}{{x - {x_0}}}$$

当$N$沿曲线$C$趋于点$M$时，$y→y_0,x→x_0;(y-y_0 )→0,(x-x_0)→0$;割线的斜率的表达式当$x→x_0$时是两个无穷小的比较，根据第一章无穷小的比较:

如果$\lim \frac{\beta }{\alpha } = 0,$，就说$β$是比$α$高阶的无穷小，记作$β=o(α).$

如果$\lim \frac{\beta }{\alpha } = \infty ,$，就说$β$是比$α$低阶的无穷小.

如果$\lim \frac{\beta }{\alpha } = c \ne 0,$，就说$β$与$α $是同阶的无穷小.

如果$\lim \frac{\beta }{{{\alpha ^k}}} = c \ne 0(k > 0)$，就说$β$是关于$α$的$k$阶无穷小.

如果$\lim \frac{\beta }{\alpha } = 1,$，就说$β$与$α$是等价无穷小，记作$\alpha \sim \beta $.

可知该比值可能等于0、1、$c$或$∞$，与这些斜率对应的直线就是曲线$C$上该点处的切线.

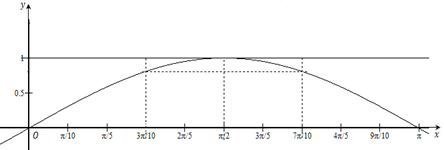
曲线上某点的切线的概念是人们在“化曲为直”的过程中建立起来的，从极限的定义出发，在几何上，曲线上某点处的自变量从该点向左右两端移动相同距离时，切线上的点到切线的距离相等.例如，函数$f(x) = \sin x,x = \frac{\pi }{2}$处的切线为$y=1$，在$x = \frac{\pi }{2}$左右两侧等距离的点$x = \frac{{3\pi }}{{10}}$和$x = \frac{{7\pi }}{{10}}$处，切线上的点到曲线的距离相等.

导数的定义

导数的英文单词是derivative.

Derivative - n. [数] 导数，微商[化] 衍生物，派生物； [语]派生词adj. 衍生的；导出的 Derive [de (down) + riv (river - n. 河，江； 溪，巨流)] + ate [v.suffux] + ive [n. &adj.suffix]

从导数的英文单词的词根分析可知，导数是to flow，pour out from its source.导数是派生，衍生出来的数，是“微商”（微小的变化量之商），是以除法（比）的形式衍生的数.

非匀速同向直线运动的瞬时速度和切线的斜率都归结为如下的极限：

$$\mathop {\lim }\limits_{x \to {x_0}} \frac{{f(x) - f({x_0})}}{{x - {x_0}}}$$

其中$x-x_0$与$f(x)-f(x_0)$分别是函数$y=f(x)$的自变量的增量$\Delta x$和函数的增量$\Delta y$.电流强度、角速度、线密度等自然科学和工程技术中的许多概念，都可以归结为上面的极限形式.抛开具体意义，从数量关系来看，就得到导数的概念.

定义 设函数$y=f(x)$在点$x_0$的某个邻域内有定义，当自变量$x$在$x_0$处取得增量$\Delta x$（点$x = {x_0} + \Delta x$仍然在该邻域内）时，相应的函数取得增量$\Delta y = f({x_0} + \Delta x) - f({x_0})$；如果$\Delta y$与$\Delta x$之比当$\Delta x \to 0$时的极限存在，则称函数$y=f(x)$在点$x_0$处可导①,并称这个极限为函数$y=f(x)$在点$x_0$处的导数，记为$f' (x_0)$，即 $$f'({x_0}) = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{\Delta y}}{{\Delta x}} = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{f({x_0} + \Delta x) - f({x_0})}}{{\Delta x}}$$ 也可以记作$$y'{|_{x = {x_0}}},\frac{{{\bf{d}}y}}{{{\bf{d}}x}}{|_{x = {x_0}}},或\frac{{{\bf{d}}f(x)}}{{{\bf{d}}x}}{|_{x = {x_0}}}$$

①可导：can be poured，flowed out from its source. 因为$\Delta x$是在$x_0$的某个邻域$U(x_0)$内，且没有特别限制，因此$x→x_0$是同时从$x_0$的左右两侧趋近$x_0$的；如果从左侧趋近的导数和从右侧趋近的导数不相同，那么函数在该点不可导.

从函数$y=f(x)$在点$x_0$的导数的定义式看出，导数是函数在以$x_0$和${x_0} + \Delta x$为端点的区间上的平均变化率在$x→x_0$时的极限，也就是函数在$x_0$点处的变化率. 函数在以$x_0$和${x_0} + \Delta x$为端点的区间上的平均变化率是函数随自变量的变化而变化的快慢程度,也就是单位自变量内函数的变化大小/变化率（例如：单位时间内位移的改变量）. $x→x_0$时，也就是函数在$x_0$点处单位自变量内函数的变化率.

上面讲的是函数在一点处可导.如果函数在区间$I$内每点处都可导，就称函数$f(x)$在该区间内可导. 这时，对于任一$x∈I$，都对应着$f(x)$的一个确定的导数值，这样就构成了一个新的函数，这个函数叫做原来函数的导函数，记作$$y',f' (x),\frac{{{\bf{d}}y}}{{{\bf{d}}x}},\frac{{{\bf{d}}f(x)}}{{{\bf{d}}x}}$$

导函数简称导数.

注意，$\frac{{{\bf{d}}y}}{{{\bf{d}}x}}$中的${\bf{d}}$是英文微分（Differential）的第一个字母，${\bf{d}}y$是函数$y$的微分，即函数$y$的微小变化量，或函数$y$的很微小的小部分.(微分的概念将在后面学习)

$$\frac{{{\bf{d}}y}}{{{\bf{d}}x}} = f'(x)$$

所以${\bf{d}}y=f' (x){\bf{d}}x.$