

我们知道,气体是由一个个分子组成的.那么,由千百万个分子组成的气体,其宏观性质自然也应该与每一个微观分子的运动息息相关.但是很显然,由于分子数量太大,用牛顿力学来解释系统内每一个分子的运动,实际上是不可能的.为了建立气体分子的微观运动与宏观现象之间的理论联系,从19世纪中叶开始,人们逐渐建立了一门新的学科——气体分子运动论.
气体分子运动论认为,气体中的大量分子处在混乱的运动之中.而整个体系所表现出来的宏观性质,可以根据力学定律以及大量分子运动所表现出来的统计规律来说明.例如,气体的压强是由大量分子撞击容器的器壁而产生的,气体温度的升高是分子平均动能增加的结果.
现在看来,上面这些东西似乎都很简单,我们在中学物理课本上就已经对它们很熟悉了.可是当分子运动论在19世纪中叶刚刚出现的时候,它却引起了一场轩然大波.玻尔兹曼就是这场风波的主角之一,并为此付出了生命的代价.
1863年,玻尔兹曼进入著名的维也纳大学学习物理学和数学专业.大学毕业后,他继续攻读博士学位.1866年2月6日,不满22岁的玻尔兹曼完成了他的博士论文《力学在热力学第二定律中的地位和作用》.在论文中,他试图利用分子运动和相互碰撞来阐述热力学第二定律,但并没有得到满意的结果.
1866年,著名物理学家麦克斯韦连续发表了两篇关于气体分子运动论方面的论文,首次引入了统计学思想,并计算出了分子速度的麦克斯韦分布律.玻尔兹曼受其启发,也转向研究分子运动论.经过两年的研究,1868年,他在《关于运动质点活力平衡研究》一文中,推广了麦克斯韦的结果,证明了在有势的力场中处于热平衡的分子运动速度分布律,即现在所称的麦克斯韦——玻尔兹曼分布律.由于这一成果,玻尔兹曼获得了在大学任教的资格.1869年,他受聘于奥地利的格拉茨大学,继任著名物理学家、哲学家马赫的数学物理学讲师职位.
1872年,玻尔兹曼对气体从不平衡过渡到平衡的过程进行了研究,导出了著名的玻尔兹曼方程.1877年,玻尔兹曼又发表了“第二定律与机械热理论的关系以及热平衡定律的概率计算”这一长篇论文,建立了热力学第二定律与概率论规律之间的直接联系,这就是玻尔兹曼熵公式.
要解释玻尔兹曼熵公式,我们先来了解一下熵的概念.熵在希腊语中是“变化”的意思,它是1854年由德国科学家克劳修斯首先引进到物理学中的,用来说明热力学过程的不可逆性.克劳修斯是从宏观热力学角度来研究熵的.所谓“宏观”,也就是说,我们是用温度、热量、体积、压强等宏观物理量来描述所研究的体系.克劳修斯把熵同系统的热量交换联系在了一起,系统熵的变化就等于热量变化除以绝对温度后所得的熵.
我们大家都知道热力学第二定律:在没有外界做功的情况下,热永远不能由冷的物体传向热的物体.利用熵的概念,我们可以把热力学第二定律表示成更简洁的说法:在孤立系统中,熵总是不断趋于增大.
那么,从微观角度看,熵又代表了什么呢?玻尔兹曼给出了他的答案:熵就是无序度.我们前面已经说过,气体内分子的数目是非常大的,我们根本不可能描述每一个分子的运动.为了解决这个难题,玻尔兹曼利用了统计的观念,用考察分子运动排列的概率来对相关物理量进行研究.
所谓概率,其实就是可能性.气体里的大量运动分子,总是有的向东有的向西,各个方向都有.对于某个分子而言,它向哪个方向运动都有可能,也就是都有一定的概率.但由于条件的限制,分子在不同方向上运动的概率是不同的.如果我们确定了这些概率,我们就能运用统计规律,得出相应的结果.例如,对于包围你的室内空气而言,就可以计算每个空气分子所有可能的分布方式及其所有可能的运动方式.这就是玻尔兹曼的思想——用统计理论来解释热力学问题,这在当时的物理学界引起了很大的争议.但事实证明,玻尔兹曼是对的.
要在热力学中计算分子处于某个微观状态的概率,首先要计算体系中粒子可能具有的所有不同微观状态的总数,它是一个非常大的数.在1877年的论文中,玻尔兹曼发现了微观状态数与宏观系统的克劳修斯熵之间的关系,并用下面这个关系式把它们联系了起来:
$$S \propto \ln W$$微观状态:系统中每一个微粒的各种状态量,比如位置,动量等.
宏观状态:系统的宏观描述,比如P,V,或者速率在某一范围内的粒子数量等.
一般来说,宏观状态包含了大量的微观状态.例如,一个容器内含有2个气体分子,我们想确认这两个气体分子在容器的左边还是右边,

宏观状态:3种:一左一右,左左,右右
微观状态:4种:LL, RR, LR, RL
3个分子时,
宏观状态:4种
微观状态:8种:LLL, (LLR, LRL, RLL), (LRR, RLR, RRL), RRR
4个分子时,
宏观状态:5种
微观状态:16种:(all L) (3L, 1R) (2L, 2R) (1L, 3R) (all R)
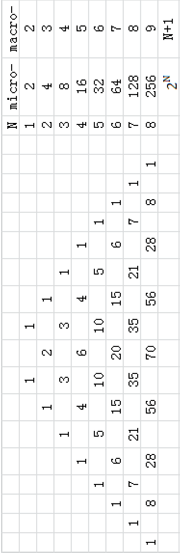
左上表可以用组合数来给出,即从N个元素中任意拿出2个,一共有多少种组合,
$${W_{N,n}} = \frac{{N!}}{{n!\left( {N - n} \right)!}}$$ $${W_{6,2}} = \frac{{6!}}{{2!4!}} = 15$$问题1:从字母a,b,c中任选两个组合,有多少种不同的选法?
ab,ac,bc 无顺序
问题2:从字母a,b,c中任选两个排成一列,有多少种不同的选法?
$A_3^2 = 6$有顺序
组合的定义:
从n个不同元素中,任取m(m≤n)个元素并成一组,叫做从n个不同元素中取出m个元素的一个组合;从n个不同元素中取出m(m≤n)个元素的所有组合的个数,叫做从n个不同元素中取出m个元素的组合数.
用符号
$$C_n^m$$表示.
排列的定义:
从n个不同元素中,任取m(m≤n)个元素按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列;从n个不同元素中取出m(m≤n)个元素的所有排列的个数,叫做从n个不同元素中取出m个元素的排列数,
用符号
$$A_n^m$$表示.
排列与组合的异同:
排列与元素的顺序有关,而组合则与元素的顺序无关.
写出从a,b,c,d四个元素中任取三个元素的所有组合.
abc
abd
acd
bcd
写出从 a,b,c,d四个元素中任取三个元素的所有排列.

求$A_4^3$可分两步考虑:
第一步,$C_4^3 = 4$
第二步,$A_3^3 = 6$
根据分步计算的原理:
$$A_4^3 = C_4^3 \cdot A_3^3$$从而
$$C_4^3 = \frac{{A_4^3}}{{A_3^3}}$$从n个不同元中取出m个元素的排列数
$$A_n^m = C_n^m \cdot A_m^m$$组合数公式:
$$\eqalign{ & C_n^m = \frac{{A_n^m}}{{A_m^m}} \cr & = \frac{{n\left( {n - 1} \right)\left( {n - 2} \right)...\left( {n - m + 1} \right)}}{{m!}} \cr & C_n^m = \frac{{n!}}{{m!\left( {n - m} \right)!}} \cr} $$原体积为${V_1}$,在更小的体积${V_f}$中找到一个气体分子的概率与体积成正比,
$$\frac{{{V_f}}}{{{V_1}}}$$在${V_f}$中找到N个气体分子的概率是找到每1个分子的概率的乘积
$${\left( {\frac{{{V_f}}}{{{V_1}}}} \right)^N}$$ $$probability = p = \frac{{{W_f}}}{{{W_1}}} = {\left( {\frac{{{V_f}}}{{{V_1}}}} \right)^N}$$取对数得
$$\ln \frac{{{W_f}}}{{{W_1}}} = N\ln \frac{{{V_f}}}{{{V_1}}}$$对理想气体,
$$\Delta S = nR\ln \frac{{{V_f}}}{{{V_1}}}$$(自己计算过程,理想气体状态方程:$pV = nRT$,则
$$\eqalign{ & \Delta S = {S_f} - {S_1} \cr & = k\ln {W_f} - k\ln {W_1} \cr} $$使用对数的原因是:1.使熵具有合理的大小;2.有利于两个状态的合并.
1990年,物理学家普朗克引进了一个比例系数,将上式写为 .这就是我们现在习惯使用的玻尔兹曼熵公式,其中$k = 1.38 \times {10^{ - 23}}$焦耳/开.为了纪念玻尔兹曼,我们把它称为玻尔兹曼常数.
根据玻尔兹曼熵公式,熵越大,W也就越大,即微观态数越多,也就是说,分子可以处在更多的微观状态.从宏观上看,整个系统就越混乱越无序.由此,我们可以看出熵的微观意义:熵是分子运动或排列混乱程度的衡量尺度,或者说,熵是系统内分子热运动无序性的量度.
玻尔兹曼熵公式直接沟通了热力学系统的宏观与微观之间的关联,并对热力学第二定律进行了微观解释.原来,热力学第二定律仅仅表明,如果没有外界的干涉,一个孤立的系统总是会越来越混乱.正像懒人的房间,如果没有人替他收拾打扫,只会越来越杂乱下去,决不会自然变得整齐起来.