梯度

如果函数$f\left( {x,y,z} \right)$在点$\left( {{x_0},{y_0},{z_0}} \right)$可微分，那么函数在该点沿任一方向l的方向导数存在，且有

$$\eqalign{ & \frac{{\partial f}}{{\partial l}}\left| {_{({x_0},{y_0},{z_0})}} \right. = \cr & {f_x}\left( {{x_0},{y_0},{z_0}} \right)\cos \alpha \cr & + \cr & {f_y}\left( {{x_0},{y_0},{z_0}} \right)\cos \beta \cr & + \cr & {f_z}\left( {{x_0},{y_0},{z_0}} \right)\cos \gamma \cr} $$

其中$\cos \alpha ,\cos \beta ,\cos \gamma $是方向l的方向余弦.（沿l方向的单位向量在$x,y,z$轴方向的投影） 称

$$\nabla = \frac{\partial }{{\partial x}}i + \frac{\partial }{{\partial y}}j + \frac{\partial }{{\partial z}}k$$

记为grad为（三维）向量微分算子或Nabla算子

$$\eqalign{ & {\text{grad }}f\left( {{x_0},{y_0},{z_0}} \right) \cr & = \cr & \nabla f\left( {{x_0},{y_0},{z_0}} \right) \cr & = \cr & {f_x}\left( {{x_0},{y_0},{z_0}} \right)i \cr & + \cr & {f_y}\left( {{x_0},{y_0},{z_0}} \right)j \cr & + \cr & {f_z}\left( {{x_0},{y_0},{z_0}} \right)k \cr} $$

为函数$f\left( {x,y,z} \right)$在点$\left( {{x_0},{y_0},{z_0}} \right)$的梯度.

则有

$$\eqalign{ & \frac{{\partial f}}{{\partial l}}\left| {_{({x_0},{y_0},{z_0})}} \right. = \cr & {f_x}\left( {{x_0},{y_0},{z_0}} \right)\cos \alpha \cr & + \cr & {f_y}\left( {{x_0},{y_0},{z_0}} \right)\cos \beta \cr & + \cr & {f_z}\left( {{x_0},{y_0},{z_0}} \right)\cos \gamma \cr & = {\text{grad}}f\left( {{x_0},{y_0},{z_0}} \right) \cdot {e_l} \cr & = \left| {{\text{grad}}f\left( {{x_0},{y_0},{z_0}} \right)} \right|\cos \theta \cr} $$

当$\theta = 0$时，即方向${e_l}$与梯度${\text{grad}}f\left( {{x_0},{y_0},{z_0}} \right)$的方向相同时，函数$f\left( {x,y,z} \right)$增加最快.此时函数在这个方向的导数达到最大值，这个最大值就是${\text{grad}}f\left( {{x_0},{y_0},{z_0}} \right)$的模.

散度

设向量值函数

$$\eqalign{ & f\left( {x,y,z} \right) = \cr & P\left( {x,y,z} \right)i \cr & + \cr & Q\left( {x,y,z} \right)j \cr & + \cr & R\left( {x,y,z} \right)k \cr} $$

它在任意一点处的散度定义为

$$\eqalign{ & {\text{div }}f\left( {x,y,z} \right) \cr & = \nabla \cdot f \cr & = \frac{{\partial P}}{{\partial x}} + \frac{{\partial Q}}{{\partial y}} + \frac{{\partial R}}{{\partial z}} \cr} $$

散度的意义

我们来考虑一个水流的向量场$a\left( r \right)$，该向量的模等于单位时间内通过垂直于向量$a\left( r \right)$的单位面积的水的质量.在向量场中取一微小体积${\text{d}}V$，现在来求流入和流出${\text{d}}V$的水的净质量.作为特例，我们考虑空间直角坐标系中的微小体积${\text{d}}V = {\text{d}}x{\text{d}}y{\text{d}}z$.

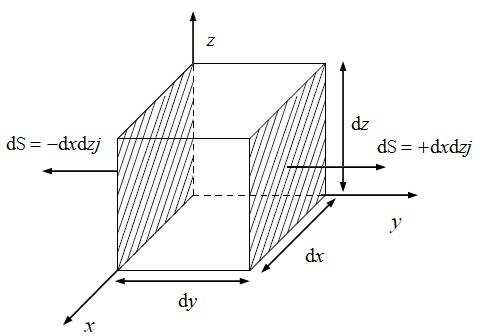
首先来看垂直于$y$轴并面向$y$轴负半轴方向的面积${\text{d}}z{\text{d}}x$，${\text{dS = }} - {\text{d}}z{\text{d}}xj$，向量$a\left( r \right)$垂直于该面积元的分量是$a\left( r \right) \cdot j = {a_y}$，方向沿$y$轴正向，通过该面积元流出去的水的质量

$$a\left( r \right) \cdot {\text{dS = }} - {a_y}{\text{d}}z{\text{d}}x$$

同理，与它正对面的面积元上流出去的水的质量为

$$a\left( r \right) \cdot {\text{dS = }}{a_y}{\text{d}}z{\text{d}}x$$

还要考虑到沿$y$轴正向增加的量${\text{ }}{a_y}{\text{d}}y{\text{d}}z{\text{d}}x$，所以从这两个面积元流出去的总质量是

$$\eqalign{ & - {a_y}{\text{d}}z{\text{d}}x + {\text{ }}{a_y}{\text{d}}z{\text{d}}x + {a_y}{\text{d}}y{\text{d}}z{\text{d}}x \cr & = {a_y}{\text{d}}y{\text{d}}z{\text{d}}x \cr} $$

$a\left( r \right) = {a_x}i + {a_y}j + {a_z}k$，${a_y}$是水流的向量场$a\left( r \right)$在$y$轴方向的分量，这个量沿$y$轴的偏导数乘以${\text{d}}y$就是水流在${\text{d}}y$长度上的量，所以${a_y}{\text{d}}y = \frac{{\partial {a_y}}}{{\partial y}}{\text{d}}y$

$${a_y} = \frac{{\partial {a_y}}}{{\partial y}}$$

所以这两个面的净流量为

$${a_y}{\text{d}}y = \frac{{\partial {a_y}}}{{\partial y}}{\text{d}}y{\text{d}}z{\text{d}}x = \frac{{\partial {a_y}}}{{\partial y}}{\text{d}}V$$

各个面的净流量加起来就是总的净流量

$$\left( {\frac{{\partial {a_x}}}{{\partial x}} + \frac{{\partial {a_y}}}{{\partial y}} + \frac{{\partial {a_z}}}{{\partial z}}} \right){\text{d}}V = \nabla \cdot a{\text{d}}V$$

则

$$\frac{{\partial {a_x}}}{{\partial x}} + \frac{{\partial {a_y}}}{{\partial y}} + \frac{{\partial {a_z}}}{{\partial z}} = \nabla \cdot a$$

由于${\text{d}}V{\text{ = d}}x{\text{d}}y{\text{d}}z$是无穷小量，上式表示向量场$a\left( r \right)$内某一点处单位体积内流出来的水的质量，称

$$\frac{{\partial {a_x}}}{{\partial x}} + \frac{{\partial {a_y}}}{{\partial y}} + \frac{{\partial {a_z}}}{{\partial z}} = \nabla \cdot a$$

为向量场$a\left( r \right)$内任意一点的散度（因为是从某一点散出来水），整个向量场的散度之和等于沿体积V的边界面的面积分（可以从电通量的概念来理解），

$$\eqalign{ & \iint\limits_V {\left( {\frac{{\partial {a_x}}}{{\partial x}} + \frac{{\partial {a_y}}}{{\partial y}} + \frac{{\partial {a_z}}}{{\partial z}}} \right){\text{d}}V} \cr & = \iint\limits_\Sigma {a\left( r \right) \cdot {\text{nd}}S} \cr} $$