当导线无限长时，${\theta _1}{\text{ = }}0,{\theta _2}{\text{ = }}\pi $，

$$B{\text{ = }}\frac{{2kI}}{a}\hat k$$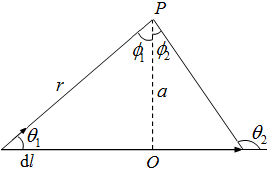

在静电学中，电场强度和场源（电荷）的关系有高斯定律

$$\Phi {\text{ = }}\mathop{{\int\!\!\!\!\!\int}\mkern-21mu \bigcirc}\limits_{\partial V} {E \cdot {\text{d}}S} {\text{ = }}\frac{1}{{{\varepsilon _0}}}\sum q {\text{ = }}\frac{Q}{{{\varepsilon _0}}}$$

也就是说，

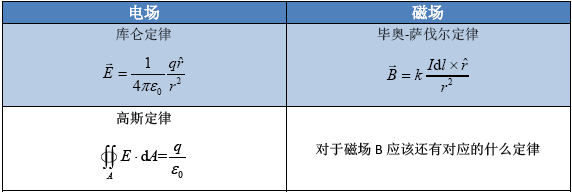
安培环路定理

在稳恒磁场中，磁感应强度$B$沿任何闭合路径的线积分，等于这闭合路径所包围的各个电流的代数和乘以磁导率.

$\oint {B \cdot {\text{d}}l{\text{ = }}{\mu _0}I} $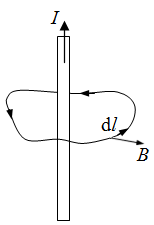

在真空中，${\mu _0}$为真空磁导率.

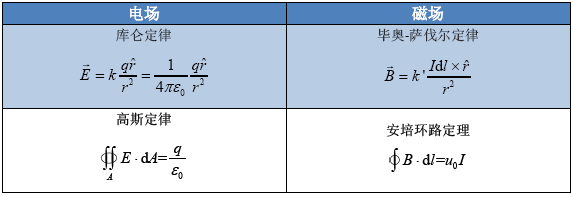
对于通电直导线周围的电场，利用安培环路定理，有

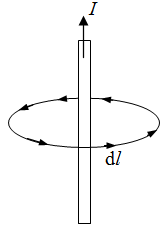$$\eqalign{ & \oint {B \cdot {\text{d}}l{\text{ = }}{u_0}I} \cr & B\oint {{\text{d}}l{\text{ = }}{u_0}I} \cr & B\left( {2\pi a} \right) = {u_0}I \cr & B = \frac{{{u_0}I}}{{2\pi a}} \cr} $$

与用毕奥-萨伐尔定律得出的电场强度

$$B{\text{ = }}\frac{{2k'I}}{a}\hat k$$