高斯定理（电通量Electric flux）大约在1837年，英国皇家学会的法拉第对静电场以及静电场与各种绝缘物质的相互作用非常感兴趣，于是设计了如下的实验：

法拉第设计了如图所示的一大一小2个同轴球体，外面一个可以分成两个半球.将外层球体分开，给内部小球带上正电荷$Q$，然后用大约2 cm 厚的“理想”绝缘物质填充在两球之间的空隙中，用外层球体盖住.接下来，外层球体迅速接地使其不带电（放电），再小心地将外层大球分开为2个半球，然后再测量两个半球上感应出的负电荷.

法拉第发现，外层球体感应出的电荷量等于内部小球体的电荷量$Q$，且与中间的绝缘物质的种类无关.他总结认为，有某种量（displacement）从内部球体流到外部球体上了，量的大小与绝缘层的种类无关.

今天，这种虽然被绝缘物质隔离但是依然从内部球体流到外部球体上的量被称为displacement flux或电通量（electric flux）.

电通量用$\Phi $表示，则

$$\Phi = Q$$

法拉第的实验可以概括为高斯定理：

通过任何闭曲面的电通量等于闭曲面内的电荷量.

假如包围电荷$Q$的曲面是任意形状的，定义$D$为电通量密度，即通过单位面积上垂直于曲面向外的电通量.

$${\Phi _M} = \int {{\text{d}}\Phi } = \iint\limits_S {D \cdot {\text{d}}S}$$

根据高斯定理，有

$${\Phi _M} = \int {{\text{d}}\Phi } = \iint\limits_S {D \cdot {\text{d}}S}{\text{ = }}Q$$

对自由空间（free space）中的一个点电荷$Q$，

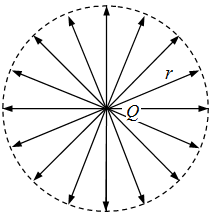
电通量密度$D = \frac{Q}{S} = \frac{Q}{{4\pi {r^2}}}$，电场强度$E = \frac{{kQ}}{{{r^2}}}$，从而$D = \frac{1}{{4\pi k}}E$，令${\varepsilon _0} = \frac{1}{{4\pi k}},k = \frac{1}{{4\pi {\varepsilon _0}}}$，则$D = {\varepsilon _0}E$

高斯定理又可以写为

$$\eqalign{ & {\Phi _M} = \int {{\text{d}}\Phi } = \iint\limits_S {{\varepsilon _0}E \cdot {\text{d}}S} \cr & {\Phi _E} = \iint\limits_S {E \cdot {\text{d}}S}{\text{ = }}\frac{Q}{{{\varepsilon _0}}} \cr} $$

由${\Phi _M} = \int {{\text{d}}\Phi } = \iint\limits_S {D \cdot {\text{d}}S}{\text{ = }}Q$，即$\Phi = DS{\text{ = }}Q$，得${\varepsilon _0} = \frac{D}{E} = \frac{Q}{{ES}}$.在学习平行板电容器时，电容$C = \frac{{\varepsilon A}}{d} = \frac{Q}{U},\varepsilon = \frac{{Qd}}{{AU}} = \frac{{Qd}}{{AEd}} = \frac{Q}{{AE}}$，$A$是平行板电容器正对极板的面积，$S$代替$A$，有$\varepsilon = \frac{Q}{{ES}}$，可见我们在上面定义的${\varepsilon _0}$与介电常数的单位相同，实际上两者就是同一个量，对于真空，称其为真空介电常数，即${\varepsilon _0}$.

我们还可以通过电场线密度的概念来推导

电荷量为$+q$的点电荷周围的电场如图所示，虚线表示以$+q$为圆心，半径为$r$的球面. 球面上任意一点的电场强度大小$E = \frac{{kq}}{{{r^2}}}$，我们知道，电场强度的大小还可以用电场线的疏密程度表示，即电场强度与穿过该点的，垂直于电场方向单位面积的电场线条数成正比，$\frac{{\Delta N}}{{\Delta A}} \propto E$.定义$\frac{{\Delta N}}{{\Delta A}}{\text{ = }}{\varepsilon _0}E$，$\Delta N{\text{ = }}{\varepsilon _0}E\Delta A$，把球面上所有面积上的电场线相加，有

$$N{\text{ = }}{\varepsilon _0}EA$$

对上面的球体，

$$N{\text{ = }}{\varepsilon _0}EA{\text{ = }}{\varepsilon _0}\frac{{kq}}{{{r^2}}} \times 4\pi {r^2} = 4\pi k{\varepsilon _0}q$$

令$k{\text{ = }}\frac{1}{{4\pi {\varepsilon _0}}}$，则有$N{\text{ = }}q$，从而穿过球面的电场线总数量等于封闭在球内的电荷量.这就是高斯定理：

垂直穿出或穿入任何闭曲面的净电场线条数在数量上等于曲面内的净电荷量.

$$N{\text{ = }}\sum {{\varepsilon _0}EA} {\text{ = }}\sum q $$